Vala 数值计算实践：月球位置算法

前言

欢迎回到 Vala 教程系列！¹

在之前的文章中，我们探讨了如何使用 Vala 语言结合 Meeus 算法来计算太阳的位置。太阳的视运动相对规律，将其视为遵循开普勒定律的二体问题（地球绕太阳公转）并辅以少量长期摄动修正项，即可获得相当高的精度。

然而，当我们把目光转向夜空中的月亮时，情况就变得复杂得多。月球的运动是著名的“三体问题”的一个实例。月球不仅受到地球引力的主导，还受到太阳引力的强烈摄动。这导致月球的轨道不是一个简单的椭圆，而是一个不断变形、进动、摆动的复杂轨迹。

本文将继续我们的 Vala 数值计算之旅，以月球位置计算为例，展示如何处理比太阳算法更复杂的数学模型，并实现一个包含视差修正和月相计算的完整月球计算器。

本文的代码实现可在 GitHub 对应仓库中获取也可以在文末查看。

界面设计与效果展示

本应用的界面设计延续了之前的教程（GTK4/Vala 教程：构建现代桌面应用）中“太阳计算器”的风格，采用了现代化的 LibAdwaita 库构建。

界面依然保持了清晰的双栏布局：左侧为参数设置与控制面板，右侧为自定义绘制的图表区域。我们同样支持了深色模式的自动适配与手动切换，以及平滑的加载动画。关于界面构建的具体细节（如 Adw.ToolbarView、Adw.PreferencesGroup 的使用，以及 Cairo 绘图的实现），请读者参考笔者之前的博客，本文不再赘述，仅在此简单展示效果截图：


浅色模式效果	深色模式效果

算法背景：月球运动的复杂性

与太阳（实际上是地球轨道）相比，月球位置的计算难度要高很多。为了提高精度，我们需要考虑更多的周期项。

月球运动本质上是一个限制性三体问题（Restricted Three-Body Problem）。在这个模型中，地球和太阳是两个主要的引力源（尽管太阳距离远，但质量巨大），而月球是一个质量相对可忽略的第三体。月球不仅受到地球引力的主导（使其绕地球公转），还受到太阳引力的强烈摄动。这些复杂的引力相互作用，可以分为两类主要效应：

短周期摄动：这些摄动项与日、地、月三者的瞬时相对位置紧密相关，周期通常在一个月或一年左右。主要包括：
- 出差 (Evection)：这是太阳摄动中对月球轨道离心率影响最大的项。其物理本质是太阳引力潮汐对月球轨道形状的周期性拉伸。当月球轨道的长轴（拱线）指向太阳时（即近地点位于朔或望），太阳引力倾向于进一步拉长轨道，导致离心率增大；反之，当长轴与太阳方向垂直时（即近地点位于上弦或下弦），太阳引力倾向于拉宽轨道（拉长短轴），导致离心率减小。这种效应的强弱取决于“日-地”连线与“地-月近地点”连线的相对夹角，其变化周期由近点月（月球相对于近地点运动周期）和朔望月（月球相对于太阳运动周期）的差异决定，本质上是这两个频率的拍频，周期约 31.8 天，振幅可达 1.274°。
出差：太阳引力导致月球轨道离心率随日-地-月相对位置发生周期性变化。
- 二均差 (Variation)：由太阳对月球的直接引力梯度效应引起。太阳引力的切向分量在月球从上/下弦运行至朔/望的过程中对月球加速，而在从朔/望运行至上/下弦的过程中对月球减速。因此，在朔（新月）和望（满月）时，月球的角速度达到最大；而在上下弦时，角速度最小。周期约为朔望月的二分之一（约14.8天）。
二均差：太阳引力的切向分量在朔望时使月球速度极大，在上下弦时速度极小。
- 周年差 (Annual Equation)：由地球绕太阳公转轨道离心率引起的月球运动周期性变化，地月系在椭圆轨道上绕日运行，与太阳的距离在近日点和远日点之间变化，导致太阳对月球轨道的潮汐摄动发生周期性变化，周期为一个近点年。
轨道自身的周期性演化：除了短周期项，月球轨道自身的几何形态也在发生着周期性的、影响更为深远的变化。这些变化描述了月球轨道的平均状态是如何“漂移”的：
- 轨道倾角 (Orbital Inclination)：月球的公转轨道平面（白道面）与地球的公转轨道平面（黄道面）并不重合，而是存在一个约 5.145° 的夹角。这个倾角是月球能够出现在黄道南北两侧的原因，是计算月球黄纬的首要参数。若无此倾角，月球将永远在黄道上运行，每个朔望月都会发生日食和月食。
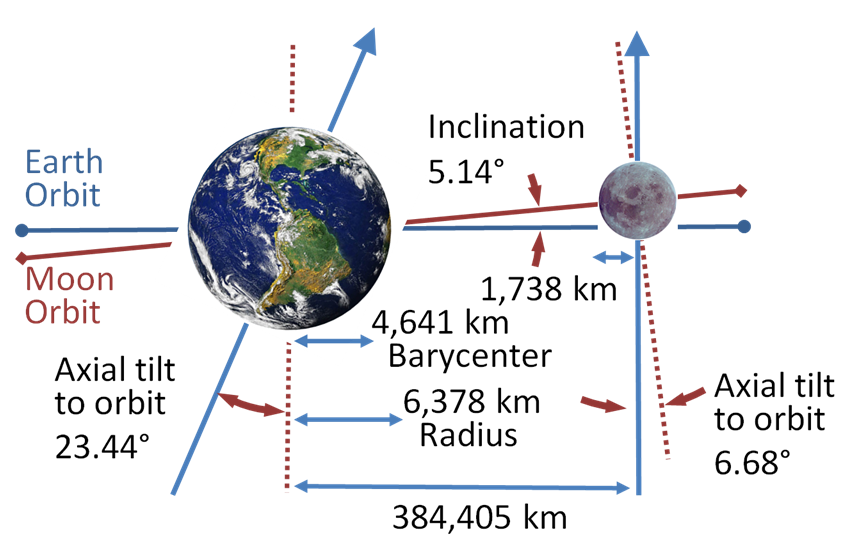
月球的轨道倾角，来自Wikipedia
- 交点退行 (Regression of the Nodes)：月球轨道与黄道的两个交点——升交点和降交点——并非固定不动。在太阳引力的作用下，这两个交点会沿着黄道向西（与月球公转方向相反）缓慢移动，每 18.6 年完成一周的退行。这一现象深刻影响着月球黄纬的计算（通过纬度参数 $F$ 体现），并且是预测日食和月食发生的关键周期，也是“沙罗周期”等概念产生的根本原因。
- 近地点进动 (Apsidal Precession)：月球轨道的近地点和远地点连成的线（拱线）也非固定。在地球非球形引力场的四极矩和太阳摄动等因素的共同作用下，它会沿着月球的公转方向向东缓慢旋转，每 8.85 年完成一周的进动。这意味着月球从一个近地点出发，再次回到近地点所需的时间（近点月）比它完成 360° 公转的时间（恒星月）要长。这一效应是修正月球平近点角 ($M’$) 和计算真实距离所必需的。
月球轨道的交点退行与近地点进动，来自Wikipedia


出差：太阳引力导致月球轨道离心率随日-地-月相对位置发生周期性变化。


二均差：太阳引力的切向分量在朔望时使月球速度极大，在上下弦时速度极小。


月球的轨道倾角，来自Wikipedia


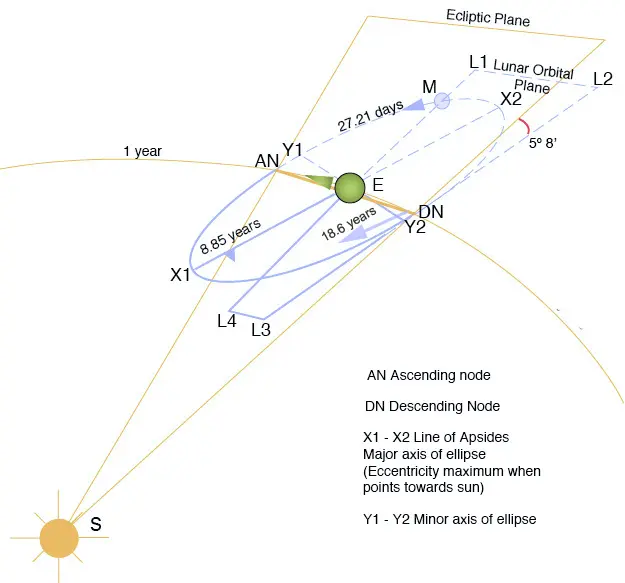
月球轨道的交点退行与近地点进动，来自Wikipedia

综合上述各类效应，月球的真实运动变得异常复杂。

在太阳算法中，我们主要关注平黄经 $L$ 和平近点角 $M$。而在月球算法中，我们需要引入五个基本参数来描述月球和太阳的相对位置及轨道状态，并通过叠加一系列三角级数项（即上述摄动效应的数学表达）来修正月球的平位置。

此外，由于月球距离地球非常近（平均约 38 万公里），地心视差（Geocentric Parallax） 的影响变得极大。对于太阳，视差仅约 8.8 角秒，通常可以忽略；而对于月球，视差可达 1 度左右（即两个满月的直径），如果不进行视差修正，计算出的地平高度将出现巨大误差。

本文采用的算法基于 Jean Meeus 的《天文算法》中的简化模型，它本质上是 ELP-2000/82 理论的一个截断版本，保留了对精度影响最大的项。

实现详解

时间基准与基本参数

首先，与太阳计算一样，我们需要计算从 J2000.0 历元（2000 年 1 月 1 日 12:00 UTC）起算的儒略世纪数 $T$。在 Vala 中，我们利用 GLib 提供的 GLib.Date 类来方便地处理日期，并将其转换为儒略日。此外 GLib 的 DateTime.get_julian () 方法返回的儒略日是从公元1年1月1日开始计算的（注意不是常见的公元前4713年），我们需要将其转换为相对于 J2000.0 的天数。

// 将 GLib.Date 转换为儒略日
var date = Date ();
date.set_dmy ((DateDay) selected_date.get_day_of_month (),
              selected_date.get_month (),
              (DateYear) selected_date.get_year ());
var julian_date = (double) date.get_julian ();

// 计算从 J2000.0 历元起算的天数和世纪数
double base_days_since_j2000 = julian_date - 730120.5;
double local_days_since_j2000 = base_days_since_j2000 + (i / 60.0 - timezone_offset_hrs) / 24.0;
double centuries_since_j2000 = local_days_since_j2000 / 36525.0;

接下来，我们需要计算月球运动的五个基本要素。这些公式是基于长期观测拟合的多项式，它们描述了月球和太阳在黄道上的平均位置及其轨道特征。在限制性三体问题中，这些参数是计算摄动项的基础变量：

月球平黄经 ($L’$)：月球在黄道上的平均位置。

\[L' = 218.3164477 + 481267.88123421 T - 0.0015786 T^2 + T^3 / 538841.0 - T^4 / 65194000.0\]

月球平距角 ($D$)：月球与太阳的平均角距离（决定了平均月相）。$D$ 决定了月球相对于“日-地”连线的位置。由于太阳的引力摄动主要取决于月球相对于太阳的方向（例如在朔望时摄动最大，上下弦时最小），$D$ 是计算出差 (Evection) 和 二均差 (Variation) 等主要摄动项的关键参数。

\[D = 297.8501921 + 445267.1114034 T - 0.0018819 T^2 + T^3 / 545868.0 - T^4 / 113065000.0\]

太阳平近点角 ($M$)：同太阳算法，描述太阳在地球轨道上的位置。$M$ 反映了地球到太阳距离的变化。由于引力与距离的平方成反比，当地月系靠近近日点时，太阳的摄动会增强。这主要影响周年差 (Annual Equation)。

\[M = 357.5291092 + 35999.0502909 T - 0.0001536 T^2 + T^3 / 24490000.0\]

月球平近点角 ($M’$)：月球在轨道上离近地点的角距离。$M’$ 描述了月球在其椭圆轨道上的位置。这是计算开普勒运动（中心天体引力主导）的主要参数，同时也与 $D$ 耦合产生复杂的摄动项。其计算公式中一次项的巨大系数，已经包含了月球自身的平均运动和近地点进动（每 8.85 年一周）的叠加效应。

\[M' = 134.9633964 + 477198.8675055 T + 0.0087414 T^2 + T^3 / 69699.0 - T^4 / 14712000.0\]

月球纬度参数 ($F$)：月球离升交点的角距离（决定了月球的黄纬）。$F$ 描述了月球相对于黄道平面的位置。太阳引力倾向于将月球拉向黄道面，导致月球轨道面的进动（交点退行）。$F$ 是计算黄纬摄动项的核心。同样，其公式体现了月球平均运动与交点退行（每 18.6 年一周）的共同影响。

\[F = 93.2720950 + 483202.0175233 T - 0.0036539 T^2 - T^3 / 3526000.0 + T^4 / 863310000.0\]

黄道坐标的周期项修正

这是月球算法中最繁琐的部分。月球的地心黄经 ($\lambda$) 和 地心黄纬 ($\beta$) 是通过在平均位置上叠加一系列周期性摄动项得到的。这些项反映了太阳引力对月球轨道的各种拉扯效应（如出差、二均差等）。

我们的代码实现选取了影响最大的几项：

黄经修正 ($\Sigma_l$)：

\[\begin{aligned} \Sigma_l = &+ 6.2888 \sin(M') \quad (\text{中心方程：椭圆轨道修正}) \\ &+ 1.2740 \sin(2D - M') \quad (\text{出差：离心率摄动}) \\ &+ 0.6583 \sin(2D) \quad (\text{二均差：切向力摄动}) \\ &+ 0.2136 \sin(2D - M) \quad (\text{地球离心率导致二均差的周年变化}) \\ &- 0.1856 \sin(M) \quad (\text{周年差：日地距离变化}) \\ &- 0.1143 \sin(2F) \quad (\text{黄道差：轨道倾角投影}) \\ &- 0.0588 \sin(2D - 2M') \quad (\text{出差二阶项}) \\ &- 0.0572 \sin(2D - M - M') \quad (\text{地球离心率导致出差的周年变化}) \\ &+ 0.0533 \sin(2D + M') \quad (\text{出差变体}) \end{aligned}\]


主要摄动项（出差、二均差、周年差）在 60 天内的变化曲线：可以看到它们具有不同的周期和振幅，共同影响着月球的黄经。

黄纬修正 ($\Sigma_b$)：

这里不仅包含了摄动项，还直接体现了月球轨道的几何特征。第一项系数 $5.1282^\circ$ 即对应了月球轨道相对于黄道的平均倾角 (Inclination)（约为 $5.145^\circ$）。由于 $F$ 包含了交点退行 (Regression of nodes) 的影响（即升交点在黄道上向西移动，周期约 18.6 年），这一项描述了月球在黄道面上下摆动的基本运动。

\[\begin{aligned} \Sigma_b = &+ 5.1282 \sin(F) \\ &+ 0.2806 \sin(M' + F) \\ &+ 0.2777 \sin(M' - F) \\ &+ 0.1732 \sin(2D - F) \end{aligned}\]

最终的地心黄道坐标为：

\[\lambda = L' + \Sigma_l\] \[\beta = \Sigma_b\]

坐标转换：从黄道到赤道

利用黄赤交角 $\epsilon$，我们将地心黄道坐标 $(\lambda, \beta)$ 转换为地心赤道坐标——赤经 ($\alpha$) 和赤纬 ($\delta$)。

\[\tan \alpha = \frac{\sin \lambda \cos \epsilon - \tan \beta \sin \epsilon}{\cos \lambda}\] \[\sin \delta = \sin \beta \cos \epsilon + \cos \beta \sin \epsilon \sin \lambda\]

地心距离计算

为了将地心坐标转换为观测者所在的站心坐标（Topocentric Coordinates），我们需要知道月球的距离。在本实现中，我们采用了更高精度的方法：先直接计算地心距离，再由距离推算视差，而非传统的先算视差再算距离的做法。这种方法的优势在于距离计算公式可以包含更多摄动修正项，从而获得更高的精度。

地心距离 ($r_{geo}$) 的计算公式（单位：千米）：

\[\begin{aligned} r_{geo} = &\, 385000.6 \quad (\text{时间平均距离}) \\ &- 20905.0 \cos(M') \quad (\text{椭圆轨道主项}) \\ &- 3699.0 \cos(2D - M') \quad (\text{出差项}) \\ &- 2956.0 \cos(2D) \quad (\text{二均差项}) \\ &- 570.0 \cos(2M') \quad (\text{椭圆轨道二阶项}) \\ &+ 246.0 \cos(2D - 2M') \quad (\text{出差二阶项}) \\ &- 205.0 \cos(2D - M) \quad (\text{地球离心率导致二均差的周年变化}) \\ &- 171.0 \cos(2D + M') \quad (\text{出差变体}) \\ &- 152.0 \cos(2D - M - M') \quad (\text{地球离心率导致出差的周年变化}) \\ \end{aligned}\]

这个公式清晰地展示了地月距离的变化规律：

常数项 $385000.6$ km：对应月球的时间平均距离。注意，这不同于月球轨道的半长轴 384399 km，在纯开普勒椭圆轨道中，时间平均距离比半长轴大，因为月球在远地点停留时间更长。对于理想的开普勒椭圆轨道，时间平均距离为 $a(1 + e^2/2)$，其中 $a$ 为半长轴，$e$ 为离心率。月球还额外受到了太阳引力的摄动，因此实际的时间平均距离在此基础上还有所增加。
$\cos(M’)$ 项（系数 $-20905.0$ km）：这是最大的变化项，反映了月球在自身椭圆轨道上运动引起的距离变化。在近地点时 $M’ \approx 0$，$\cos(M’) \approx 1$，距离减小约 20905 km；在远地点时 $M’ \approx 180°$，$\cos(M’) \approx -1$，距离增大约 20905 km。这一项完美体现了月球轨道的离心率效应。
$\cos(2D - M’)$ 项（系数 $-3699.0$ km）：出差效应对距离的贡献，反映了太阳引力对月球轨道离心率的周期性调制。
$\cos(2D)$ 项（系数 $-2956.0$ km）：二均差效应的距离分量，与月球相对于太阳的位置（朔望/上下弦）直接相关。
其他项：更精细的摄动修正，包括椭圆轨道的二阶修正、周年差等。

视差修正与站心坐标


地心视差示意图：由于观测者位于地球表面 $P$ 而非地心 $O$，观测到的月球位置会发生偏移。
图中 $z$ 为地心天顶距，$z’$ 为站心天顶距（$z = 90^\circ - El$，$z’ = 90^\circ - El’$）。
视差角 $\pi_p$ 导致 $z’ > z$（$z’ = z + \pi_p$），因此月球的站心高度角 $El’$ 小于地心高度角 $El$。

视差修正是月球计算中至关重要的一步。之前的计算都是假设观测者位于地心，但实际上观测者位于地球表面。对于月球这样近的天体，这种位置差异会导致视位置的显著改变。

有了地心距离后，我们首先计算用于视差修正的赤道地平视差 ($\pi_p$)，即地球赤道半径 $R_\oplus$ 在月球中心的张角：

\[\sin \pi_p = \frac{R_\oplus}{r_{geo}} = \frac{6378.137}{r_{geo}}\]

这个视差值大约在 $0.9°$ 到 $1°$ 之间变化。

接下来，我们需要计算观测者的地方恒星时 (LST)，然后得到时角 (H)：

\[H = \text{LST} - \alpha\]

利用视差 $\pi_p$ 和观测者的地理纬度 $\phi$，我们将地心坐标 $(\alpha, \delta)$ 转换为站心坐标 $(\alpha’, \delta’)$。地球实际上并非理想的球体，而是一个扁球体，这对较精密的计算有明显影响，因此我们需要考虑地球的扁率 $f \approx 1/298.257223563$，使用椭球模型。这里我们使用严密的矢量公式（或其分量形式）：

\[\begin{aligned} A &= \cos \delta \sin H \\ B &= \cos \delta \cos H - \rho \cos \phi' \sin \pi_p \\ C &= \sin \delta - \rho \sin \phi' \sin \pi_p \end{aligned}\]

其中 $\rho \sin \phi’$ 和 $\rho \cos \phi’$ 是考虑了地球扁率后的地心纬度函数。

于是，站心时角 $H’$ 和站心赤纬 $\delta’$ 可由下式求得：

\[\tan H' = \frac{A}{B}\] \[\tan \delta' = \frac{C}{\sqrt{A^2 + B^2}}\]

A, B, C 实际上构成了从观测者指向月球的矢量的三个分量（以地月地心距离为单位长度）。因此，从观测者到月球的真正距离——站心距离 ($r_{topo}$) ——也可以通过计算这个矢量的模长得到：

\[r_{topo} = r_{geo} \times \sqrt{A^2 + B^2 + C^2}\]

其中，$r_{geo}$ 是我们之前算出的地心距离。这正是代码中计算 moon_distances 的方法。最终程序界面上显示的，便是这个经过完整视差修正后的站心距离。由于站心距是观测者与月球的“直线距离”，它叠加了观测者在地球上的位置及地球大小的影响，因此这个值完全可以大于远地点或者小于近地点距离，这完全是合理的。

地平高度角

利用站心赤纬 $\delta’$ 和站心时角 $H’$，通过标准的球面三角公式计算出月球的地平高度角 (Elevation)：

\[\sin(\text{El}) = \sin \phi \sin \delta' + \cos \phi \cos \delta' \cos H'\]

double elevation_sin = sin_lat * Math.sin (topocentric_declination_rad)
                 + cos_lat * Math.cos (topocentric_declination_rad) * Math.cos (topocentric_hour_angle_rad);
double true_elevation_deg = Math.asin (elevation_sin.clamp (-1.0, 1.0)) * RAD2DEG;

大气折射修正

在计算出几何地平高度角后，为了获得更接近实际观测的值，我们还需要考虑大气折射（Atmospheric Refraction）的影响。大气层会使光线发生弯曲，使得天体的视高度比几何高度要高。

本程序采用了 Saemundsson 公式 来估算标准大气条件下的折射角 $R$（单位：度）：

\[R = 1.02 \cot \left( h + \frac{10.3}{h + 5.11} \right) \times \frac{1}{60}\]

其中 $h$ 是真高度角（单位：度）。值得注意的是，该公式在数学上存在适用范围。当真高度角 $h$ 过低（小于约 -5.0015°）或接近天顶（大于约 89.8915°）时，公式计算出的修正值会变为负数，不合理。因此，我们在代码中加入了范围检查，仅在 $-5.0015^\circ < h < 89.8915^\circ$ 的范围内应用此修正，超出范围则视为无折射。Saemundsson 公式精度良好，在从天顶到地平线的整个范围内，误差小于 0.1’（约 0.0017°）。

此外，由于大气折射受气温、气压等天气因素影响极大，我们在界面上提供了一个折射系数 调节选项。用户可以根据实际观测条件调整该系数（默认为 1.0，即标准大气模型；设为 0.0 则关闭修正）。

注意：下文“精度评估”一节中的对比数据是基于无大气折射的纯几何位置进行的。这是因为折射强烈受天气等因素的影响，难以进行统一的精度评估。

月相与亮面比例

除了位置，我们还计算了月相。月球的被照亮比例 $k$ 取决于日月距角 (Elongation, $\psi$)：

\[\cos \psi = \cos \beta \cos (\lambda_{moon} - \lambda_{sun})\] \[k = \frac{1 - \cos \psi}{2}\]


月相与距角：月球绕地球公转，随着日、地、月三者相对位置的变化（距角变化），地球上看到的月球亮面比例（月相）也随之改变。

这里 $\lambda_{sun}$ 是太阳的视黄经。

编译与运行

确保你的系统已安装 Vala、GTK4、LibAdwaita、JSON-GLib 以及 C 编译器。在 Linux 下，还需要额外安装在 GLib/GIO 中实现网络访问的 gvfs 库（Windows则不需要）。笔者在此列举了在 Arch Linux 和 Windows MSYS2 环境下的安装命令：

Arch Linux：

sudo pacman -S --needed vala gtk4 libadwaita json-glib gvfs

Windows MSYS2：在 MSYS2 UCRT64 环境中：

pacman -S --needed mingw-w64-ucrt-x86_64-vala mingw-w64-ucrt-x86_64-gcc mingw-w64-ucrt-x86_64-gtk4 mingw-w64-ucrt-x86_64-libadwaita mingw-w64-ucrt-x86_64-json-glib

你可以将完整代码保存为 lunarcalc.vala，可以手动保存，也可以使用以下命令下载：

wget https://raw.githubusercontent.com/wszqkzqk/FunValaGtkExamples/master/lunarcalc.vala

然后使用以下命令进行编译：

valac --pkg=gtk4 --pkg=libadwaita-1 --pkg=json-glib-1.0 -X -lm -X -O2 -X -pipe lunarcalc.vala

或者，如果你在 Linux 环境下，可以直接赋予脚本执行权限并运行（脚本头部已包含 Shebang）：

chmod +x lunarcalc.vala
./lunarcalc.vala

精度评估

为了客观评估本程序算法（基于 Jean Meeus 截断级数）的准确性，笔者将本程序的计算结果与天文学权威库 Astropy 进行了对比测试。

测试范围设定为 1975 年至 2075 年（涵盖 100 年以包含所有主要月球周期），选取了全球 6 个具有代表性的地点进行验证：北京（39.9°N, 116.4°E）、重庆（29.6°N, 106.6°E）、新加坡（1.3°N, 103.8°E）、悉尼（33.9°S, 151.2°E）、斯德哥尔摩（59.3°N, 18.1°E）以及南极点（90°S, 0°E），均不考虑大气折射。这些地点覆盖了从赤道到极地的各种纬度，能够全面检验算法在不同地理位置下的表现。笔者采集了该时间段内所有整时刻的数据，每个地点采集了约 88.5 万个数据点，总计共采集 5,312,160 个样本点进行比对。

各地点精度统计：

地点	样本数	高度角 RMSD (°)	距离 RMSD (km)	月相 RMSD
北京	885,360	0.145	167	0.0036
重庆	885,360	0.164	167	0.0039
新加坡	885,360	0.188	167	0.0043
悉尼	885,360	0.156	167	0.0038
斯德哥尔摩	885,360	0.112	167	0.0029
南极点	885,360	0.083	166	0.0023

整体统计汇总（5,312,160 个样本点）：

评估指标	均方根偏差 (RMSD)	95% 分位数误差绝对值 (95% Abs)	最大误差绝对值 (Max Abs)	误差平均值 (Mean Error)
高度角 (°)	0.146	0.308	0.586	$-1.14 \times 10^{-4}$
地月距离 (km)	167	320	525	0.0698
月相 (照明度)	0.0035	0.0073	0.0135	$1.56 \times 10^{-4}$


误差分布直方图

误差绝对值分布直方图

数据表明，本算法在极低的计算负载下实现了优异的精度平衡。从各地点的结果可以看出，高度角误差与地理纬度有一定相关性：高纬度地区（如斯德哥尔摩、南极点）的误差较小，而低纬度赤道附近地区（如新加坡）的误差相对较大。这是因为在赤道附近，天体运动轨迹垂直于地平线，地心坐标到地平坐标的转换中，时角的变化对高度角的影响最为直接和剧烈。简化算法中对月球轨道经度的误差，在赤道地区被最大程度地投影到了高度角误差上。在极地，天体运动轨迹几乎平行于地平线。经度上的计算误差主要变成了方位角误差，而对高度角的影响被几何投影缩小了。但总体上，程序表现良好：

0.15° 的高度角误差仅相当于满月视直径的三分之一，这意味着在绝大多数时间里，程序计算出的月球位置依然落在实际月球的轮廓范围内，在肉眼观测或广角摄影中几乎无法察觉差异
167 km 的距离误差（相对误差约 0.04%）完全不影响对”超级月亮”等视直径变化的判断
0.35% 的月相误差更是远超人眼辨识极限

这证明本程序虽然简化了部分微小摄动项，但依然能在摄影构图、赏月规划及科普演示等场景中，提供与专业天文年历无异的使用体验。

总结

通过上述步骤，我们用 Vala 实现了一个精度相当可观的月球位置计算器。虽然为了代码简洁性，我们省略了 ELP-2000 理论中数以千计的微小摄动项，但保留的主项足以满足一般天文观测和摄影的需求。

这个案例再次证明，Vala 凭借其 C 语言级别的性能和现代化的语法，非常适合处理此类包含大量复杂三角函数运算的科学计算任务，再加上 GTK4 和 LibAdwaita 的生态加持，我们可以轻松地将这些后台计算与流畅的 UI 交互结合起来，实时展现天体的奥秘。

完整代码实现

#!/usr/bin/env -S vala --pkg=gtk4 --pkg=libadwaita-1 --pkg=json-glib-1.0 -X -lm -X -O2 -X -march=native -X -pipe
/* SPDX-License-Identifier: LGPL-2.1-or-later */

/**
 * Lunar Calculator.
 * Copyright (C) 2025 wszqkzqk <wszqkzqk@qq.com>
 * A libadwaita application that calculates and visualizes lunar data including
 * elevation angles, distance, phase information, and other lunar parameters
 * throughout the day for a given location and date, with parallax correction.
 */
public class LunarCalc : Adw.Application {
    // Constants for math
    private const double DEG2RAD = Math.PI / 180.0;
    private const double RAD2DEG = 180.0 / Math.PI;
    private const int RESOLUTION_PER_MIN = 1440; // 1 sample per minute
    // Constants for drawing area
    private const int MARGIN_LEFT = 70;
    private const int MARGIN_RIGHT = 20;
    private const int MARGIN_TOP = 50;
    private const int MARGIN_BOTTOM = 70;
    // Default info label
    private const string DEFAULT_INFO_LABEL = "Click on the chart for details\nElevation: --\nDistance: --\nPhase: --";

    // Model / persistent state
    private DateTime selected_date;
    private double moon_angles[RESOLUTION_PER_MIN]; // Store moon elevation angles in degrees (-90 to +90)
    private double moon_phases[RESOLUTION_PER_MIN]; // Store illumination fraction (0.0 - 1.0)
    private double moon_elongations[RESOLUTION_PER_MIN];   // Store moon elongations in degrees (0 - 360)
    private double moon_distances[RESOLUTION_PER_MIN]; // Store moon distance in km
    private double latitude = 0.0;
    private double longitude = 0.0;
    private double timezone_offset_hours = 0.0;
    private double refraction_factor = 1.0;

    // Interaction / transient UI state
    private double clicked_time_hours = 0.0;
    private double corresponding_angle = 0.0;
    private bool has_click_point = false;

    // UI widgets
    private Adw.ApplicationWindow window;
    private Gtk.DrawingArea drawing_area;
    private Gtk.Label click_info_label;
    private Gtk.Stack location_stack;
    private Gtk.Spinner location_spinner;
    private Gtk.Button location_button;
    private Adw.SpinRow latitude_row;
    private Adw.SpinRow longitude_row;
    private Adw.SpinRow timezone_row;

    // Color theme struct for chart drawing
    private struct ThemeColors {
        double bg_r; double bg_g; double bg_b; // Background
        double grid_r; double grid_g; double grid_b; double grid_a; // Grid
        double axis_r; double axis_g; double axis_b; // Axes
        double text_r; double text_g; double text_b; // Text
        double curve_r; double curve_g; double curve_b; // Curve
        double shade_r; double shade_g; double shade_b; double shade_a; // Shaded area
        double point_r; double point_g; double point_b; // Click point
        double line_r; double line_g; double line_b; double line_a; // Guide line
    }

    // Light theme
    private static ThemeColors LIGHT_THEME = {
        bg_r: 1.0, bg_g: 1.0, bg_b: 1.0,                    // White background
        grid_r: 0.5, grid_g: 0.5, grid_b: 0.5, grid_a: 0.5, // Gray grid
        axis_r: 0.0, axis_g: 0.0, axis_b: 0.0,              // Black axes
        text_r: 0.0, text_g: 0.0, text_b: 0.0,              // Black text
        curve_r: 0.1, curve_g: 0.1, curve_b: 0.8,           // Blue curve
        shade_r: 0.7, shade_g: 0.7, shade_b: 0.7, shade_a: 0.3, // Light gray shade
        point_r: 0.8, point_g: 0.3, point_b: 0.0,           // Orange point
        line_r: 0.8, line_g: 0.3, line_b: 0.0, line_a: 0.5  // Orange guide lines
    };

    // Dark theme
    private static ThemeColors DARK_THEME = {
        bg_r: 0.0, bg_g: 0.0, bg_b: 0.0,                    // Black background
        grid_r: 0.5, grid_g: 0.5, grid_b: 0.5, grid_a: 0.5, // Gray grid
        axis_r: 1.0, axis_g: 1.0, axis_b: 1.0,              // White axes
        text_r: 1.0, text_g: 1.0, text_b: 1.0,              // White text
        curve_r: 0.3, curve_g: 0.7, curve_b: 1.0,           // Light blue curve
        shade_r: 0.3, shade_g: 0.3, shade_b: 0.3, shade_a: 0.7, // Dark gray shade
        point_r: 1.0, point_g: 0.5, point_b: 0.0,           // Orange point
        line_r: 1.0, line_g: 0.5, line_b: 0.0, line_a: 0.7  // Orange guide lines
    };

    /**
     * Creates a new LunarCalc instance.
     *
     * Initializes the application with a unique application ID and sets
     * the selected date to the current local date.
     */
    public LunarCalc () {
        Object (application_id: "com.github.wszqkzqk.LunarCalc");
        selected_date = new DateTime.now_local ();
    }

    /**
     * Activates the application and creates the main window.
     *
     * Sets up the user interface including input controls, drawing area,
     * and initializes the plot data with current settings.
     */
    protected override void activate () {
        window = new Adw.ApplicationWindow (this) {
            title = "Lunar Calculator",
        };

        // Create header bar
        var header_bar = new Adw.HeaderBar () {
            title_widget = new Adw.WindowTitle ("Lunar Calculator", ""),
        };

        // Add dark mode toggle button
        var dark_mode_button = new Gtk.ToggleButton () {
            icon_name = "weather-clear-night-symbolic",
            tooltip_text = "Toggle dark mode",
            active = style_manager.dark,
        };
        dark_mode_button.toggled.connect (() => {
            style_manager.color_scheme = (dark_mode_button.active) ? Adw.ColorScheme.FORCE_DARK : Adw.ColorScheme.FORCE_LIGHT;
            drawing_area.queue_draw ();
        });
        style_manager.notify["dark"].connect (() => {
            drawing_area.queue_draw ();
        });
        header_bar.pack_end (dark_mode_button);

        var toolbar_view = new Adw.ToolbarView ();
        toolbar_view.add_top_bar (header_bar);

        var main_box = new Gtk.Box (Gtk.Orientation.HORIZONTAL, 0);

        var left_scrolled = new Gtk.ScrolledWindow () {
            hscrollbar_policy = Gtk.PolicyType.NEVER,
            vscrollbar_policy = Gtk.PolicyType.AUTOMATIC,
            hexpand = false,
            vexpand = true,
            propagate_natural_height = true,
            propagate_natural_width = true,
        };

        var left_panel = new Gtk.Box (Gtk.Orientation.VERTICAL, 12) {
            margin_start = 12,
            margin_end = 12,
            margin_top = 12,
            margin_bottom = 12,
        };

        // Location and Time Settings Group
        var observer_parameters_group = new Adw.PreferencesGroup () {
            title = "Observer Parameters",
        };

        var location_detect_row = new Adw.ActionRow () {
            title = "Auto-detect Location",
            subtitle = "Get current location and timezone",
            activatable = true,
        };

        var location_box = new Gtk.Box (Gtk.Orientation.HORIZONTAL, 6);
        location_stack = new Gtk.Stack () {
            hhomogeneous = true,
            vhomogeneous = true,
            transition_type = Gtk.StackTransitionType.CROSSFADE,
        };
        location_spinner = new Gtk.Spinner ();
        location_button = new Gtk.Button () {
            icon_name = "find-location-symbolic",
            valign = Gtk.Align.CENTER,
            css_classes = { "flat" },
            tooltip_text = "Auto-detect current location",
        };
        location_button.clicked.connect (on_auto_detect_location);
        location_stack.add_child (location_button);
        location_stack.add_child (location_spinner);
        location_stack.visible_child = location_button;
        location_box.append (location_stack);
        location_detect_row.add_suffix (location_box);
        location_detect_row.activated.connect (on_auto_detect_location);

        latitude_row = new Adw.SpinRow.with_range (-90, 90, 0.1) {
            title = "Latitude",
            subtitle = "Degrees",
            value = latitude,
            digits = 2,
        };
        latitude_row.notify["value"].connect (() => {
            latitude = latitude_row.value;
            update_plot_data ();
            drawing_area.queue_draw ();
        });

        longitude_row = new Adw.SpinRow.with_range (-180.0, 180.0, 0.1) {
            title = "Longitude",
            subtitle = "Degrees",
            value = longitude,
            digits = 2,
        };
        longitude_row.notify["value"].connect (() => {
            longitude = longitude_row.value;
            update_plot_data ();
            drawing_area.queue_draw ();
        });

        timezone_row = new Adw.SpinRow.with_range (-12.0, 14.0, 0.5) {
            title = "Timezone",
            subtitle = "Hours from UTC",
            value = timezone_offset_hours,
            digits = 2,
        };
        timezone_row.notify["value"].connect (() => {
            timezone_offset_hours = timezone_row.value;
            update_plot_data ();
            drawing_area.queue_draw ();
        });

        var refraction_row = new Adw.SpinRow.with_range (0.0, 2.0, 0.05) {
            title = "Refraction",
            subtitle = "Correction level",
            tooltip_text = "Set to 1.0 for standard atmosphere.\nSet to 0.0 to disable refraction.",
            value = refraction_factor,
            digits = 2,
        };
        refraction_row.notify["value"].connect (() => {
            refraction_factor = refraction_row.value;
            update_plot_data ();
            drawing_area.queue_draw ();
        });

        observer_parameters_group.add (location_detect_row);
        observer_parameters_group.add (latitude_row);
        observer_parameters_group.add (longitude_row);
        observer_parameters_group.add (timezone_row);
        observer_parameters_group.add (refraction_row);

        // Date Selection Group
        var date_group = new Adw.PreferencesGroup () {
            title = "Date Selection",
        };
        var calendar = new Gtk.Calendar () {
            margin_start = 20,
            margin_end = 20,
            margin_top = 6,
            margin_bottom = 6,
        };
        calendar.day_selected.connect (() => {
            selected_date = calendar.get_date ();
            update_plot_data ();
            drawing_area.queue_draw ();
        });
        var calendar_row = new Adw.ActionRow ();
        calendar_row.child = calendar;
        date_group.add (calendar_row);

        // Click Info Group
        var click_info_group = new Adw.PreferencesGroup () {
            title = "Lunar Info",
        };

        click_info_label = new Gtk.Label (DEFAULT_INFO_LABEL) {
            halign = Gtk.Align.START,
            margin_start = 12,
            margin_end = 12,
            margin_top = 6,
            margin_bottom = 6,
            wrap = true,
        };

        var click_info_row = new Adw.ActionRow ();
        click_info_row.child = click_info_label;
        click_info_group.add (click_info_row);

        // Export Group
        var export_group = new Adw.PreferencesGroup () {
            title = "Export",
        };
        var export_image_row = new Adw.ActionRow () {
            title = "Export Image",
            subtitle = "Save chart as PNG, SVG, or PDF",
            activatable = true,
        };
        var export_image_button = new Gtk.Button () {
            icon_name = "document-save-symbolic",
            valign = Gtk.Align.CENTER,
            css_classes = { "flat" },
        };
        export_image_button.clicked.connect (on_export_clicked);
        export_image_row.add_suffix (export_image_button);
        export_image_row.activated.connect (on_export_clicked);

        var export_csv_row = new Adw.ActionRow () {
            title = "Export CSV",
            subtitle = "Save data as CSV file",
            activatable = true,
        };
        var export_csv_button = new Gtk.Button () {
            icon_name = "x-office-spreadsheet-symbolic",
            valign = Gtk.Align.CENTER,
            css_classes = { "flat" },
        };
        export_csv_button.clicked.connect (on_export_csv_clicked);
        export_csv_row.add_suffix (export_csv_button);
        export_csv_row.activated.connect (on_export_csv_clicked);

        export_group.add (export_image_row);
        export_group.add (export_csv_row);

        left_panel.append (observer_parameters_group);
        left_panel.append (date_group);
        left_panel.append (click_info_group);
        left_panel.append (export_group);
        left_scrolled.child = left_panel;

        drawing_area = new Gtk.DrawingArea () {
             hexpand = true,
             vexpand = true,
             width_request = 600,
             height_request = 500,
         };
        drawing_area.set_draw_func (draw_lunar_angle_chart);

        var click_controller = new Gtk.GestureClick ();
        click_controller.pressed.connect (on_chart_clicked);
        drawing_area.add_controller (click_controller);

        main_box.append (left_scrolled);
        main_box.append (drawing_area);

        toolbar_view.content = main_box;

        update_plot_data ();

        window.content = toolbar_view;
        window.present ();
    }

    /**
     * Handles auto-detect location button click.
     *
     * Uses a free IP geolocation service to get current location and timezone.
     */
    private void on_auto_detect_location () {
        location_button.sensitive = false;
        location_stack.visible_child = location_spinner;
        location_spinner.start ();

         get_location_async.begin ((obj, res) => {
            try {
                get_location_async.end (res);
            } catch (Error e) {
                show_error_dialog ("Location Detection Failed", e.message);
            }
            location_button.sensitive = true;
            location_spinner.stop ();
            location_stack.visible_child = location_button;
         });
    }

    /**
     * Asynchronously gets current location using IP geolocation service with timeout.
     *
     * @throws IOError If location detection fails.
     */
    private async void get_location_async () throws IOError {
        var file = File.new_for_uri ("https://ipapi.co/json/");
        var parser = new Json.Parser ();
        var cancellable = new Cancellable ();
        var timeout_id = Timeout.add_seconds_once (5, () => { cancellable.cancel (); });

        try {
            var stream = yield file.read_async (Priority.DEFAULT, cancellable);
            yield parser.load_from_stream_async (stream, cancellable);
        } catch (Error e) {
            throw new IOError.FAILED ("Failed to get location: %s", e.message);
        } finally {
            if (!cancellable.is_cancelled ()) Source.remove (timeout_id);
        }

        var root_object = parser.get_root ().get_object ();
        if (root_object.get_boolean_member_with_default ("error", false)) {
            throw new IOError.FAILED ("Location service error: %s", root_object.get_string_member_with_default ("reason", "Unknown error"));
        }

        if (root_object.has_member ("latitude") && root_object.has_member ("longitude")) {
            latitude = root_object.get_double_member ("latitude");
            longitude = root_object.get_double_member ("longitude");
        } else {
            throw new IOError.FAILED ("No coordinates found");
        }

        double network_tz_offset = 0.0;
        bool has_network_tz = false;
        if (root_object.has_member ("utc_offset")) {
            var offset_str = root_object.get_string_member ("utc_offset");
            network_tz_offset = double.parse (offset_str) / 100.0;
            has_network_tz = true;
        }

        var timezone = new TimeZone.local ();
        var time_interval = timezone.find_interval (GLib.TimeType.UNIVERSAL, selected_date.to_unix ());
        var local_tz_offset = timezone.get_offset (time_interval) / 3600.0;

        const double TZ_EPSILON = 0.01;
        const string NETWORK_CHOICE = "network";
        const string LOCAL_CHOICE = "local";
        if (has_network_tz && (!(-TZ_EPSILON < (network_tz_offset - local_tz_offset) < TZ_EPSILON))) {
            var dialog = new Adw.AlertDialog (
                "Timezone Mismatch",
                "The timezone from the network (UTC%+.2f) differs from your system's timezone (UTC%+.2f).\n\nWhich one would you like to use?".printf (network_tz_offset, local_tz_offset)
            );
            dialog.add_response (NETWORK_CHOICE, "Use Network Timezone");
            dialog.add_response (LOCAL_CHOICE, "Use System Timezone");
            dialog.default_response = NETWORK_CHOICE;
            unowned var choice = yield dialog.choose (window, null);
            timezone_offset_hours = (choice == NETWORK_CHOICE) ? network_tz_offset : local_tz_offset;
        } else {
            timezone_offset_hours = local_tz_offset;
        }

        latitude_row.value = latitude;
        longitude_row.value = longitude;
        timezone_row.value = timezone_offset_hours;
        update_plot_data ();
        drawing_area.queue_draw ();
    }

    /**
     * Shows a generic error dialog and logs the error message.
     *
     * @param title The title of the error dialog.
     * @param error_message The error message to display.
     */
    private void show_error_dialog (string title, string error_message) {
        var dialog = new Adw.AlertDialog (title, error_message);
        dialog.add_response ("ok", "OK");
        dialog.present (window);
        message ("%s: %s", title, error_message);
    }

    /**
     * Gets the phase description string based on elongation angle.
     *
     * @param phase_fraction Illuminated fraction (0.0-1.0).
     * @param elongation_deg Elongation angle in degrees.
     * @return Phase description string.
     */
    private string get_phase_description (double phase_fraction, double elongation_deg) {
        while (elongation_deg < 0) elongation_deg += 360.0;
        while (elongation_deg >= 360.0) elongation_deg -= 360.0;

        string desc;
        if (elongation_deg < 5 || elongation_deg > 355) desc = "New Moon";
        else if (elongation_deg < 85) desc = "Waxing Crescent";
        else if (elongation_deg < 95) desc = "First Quarter";
        else if (elongation_deg < 175) desc = "Waxing Gibbous";
        else if (elongation_deg < 185) desc = "Full Moon";
        else if (elongation_deg < 265) desc = "Waning Gibbous";
        else if (elongation_deg < 275) desc = "Last Quarter";
        else desc = "Waning Crescent";

        return "%s (%.1f%%)".printf(desc, phase_fraction * 100.0);
    }

    /**
     * Calculates Moon elevation angles and phases for each minute of the day.
     * Includes parallax correction. No atmospheric refraction.
     *
     * @param latitude_rad Latitude in radians.
     * @param longitude_deg Longitude in degrees.
     * @param timezone_offset_hrs Timezone offset from UTC in hours.
     * @param julian_date GLib's Julian Date for the day (from 0001-01-01).
     */
    private void generate_moon_angles (double latitude_rad, double longitude_deg, double timezone_offset_hrs, double julian_date) {
        double earth_flattening = 1.0 / 298.257223563;
        double phi_prime = Math.atan ((1 - earth_flattening) * Math.tan (latitude_rad));
        double rho_sin_phi_prime = (1 - earth_flattening) * Math.sin (phi_prime);
        double rho_cos_phi_prime = Math.cos (phi_prime);

        double sin_lat = Math.sin (latitude_rad);
        double cos_lat = Math.cos (latitude_rad);

        // Base days from J2000.0 epoch (GLib's Julian Date is days since 0001-01-01 12:00 UTC)
        double base_days_since_j2000 = julian_date - 730120.5;

        // Pre-compute obliquity that changes very slowly
        double base_centuries_since_j2000 = base_days_since_j2000 / 36525.0;
        double base_centuries_since_j2000_sq = base_centuries_since_j2000 * base_centuries_since_j2000;
        double base_centuries_since_j2000_cu = base_centuries_since_j2000_sq * base_centuries_since_j2000;
        double obliquity_deg = 23.439291111 - 0.013004167 * base_centuries_since_j2000 - 1.63889e-7 * base_centuries_since_j2000_sq + 5.0361e-7 * base_centuries_since_j2000_cu;
        double obliquity_rad = obliquity_deg * DEG2RAD;
        double obliquity_sin = Math.sin (obliquity_rad);
        double obliquity_cos = Math.cos (obliquity_rad);
        double sun_eq_c1 = 1.914602 - 0.004817 * base_centuries_since_j2000 - 0.000014 * base_centuries_since_j2000_sq;
        double sun_eq_c2 = 0.019993 - 0.000101 * base_centuries_since_j2000;

        for (int i = 0; i < RESOLUTION_PER_MIN; i += 1) {
            double local_days_since_j2000 = base_days_since_j2000 + (i / 60.0 - timezone_offset_hrs) / 24.0;
            double centuries_since_j2000 = local_days_since_j2000 / 36525.0;
            double centuries_since_j2000_sq = centuries_since_j2000 * centuries_since_j2000;
            double centuries_since_j2000_cu = centuries_since_j2000_sq * centuries_since_j2000;
            double centuries_since_j2000_q = centuries_since_j2000_cu * centuries_since_j2000;

            double moon_mean_longitude_deg = 218.3164477 + 481267.88123421 * centuries_since_j2000 - 0.0015786 * centuries_since_j2000_sq + centuries_since_j2000_cu / 538841.0 - centuries_since_j2000_q / 65194000.0;
            double mean_elongation_deg = 297.8501921 + 445267.1114034 * centuries_since_j2000 - 0.0018819 * centuries_since_j2000_sq + centuries_since_j2000_cu / 545868.0 - centuries_since_j2000_q / 113065000.0;
            double sun_mean_anomaly_deg = 357.5291092 + 35999.0502909 * centuries_since_j2000 - 0.0001536 * centuries_since_j2000_sq + centuries_since_j2000_cu / 24490000.0;
            double moon_mean_anomaly_deg = 134.9633964 + 477198.8675055 * centuries_since_j2000 + 0.0087414 * centuries_since_j2000_sq + centuries_since_j2000_cu / 69699.0 - centuries_since_j2000_q / 14712000.0;
            double moon_argument_of_latitude_deg = 93.2720950 + 483202.0175233 * centuries_since_j2000 - 0.0036539 * centuries_since_j2000_sq - centuries_since_j2000_cu / 3526000.0 + centuries_since_j2000_q / 863310000.0;

            double mean_elongation_rad = mean_elongation_deg * DEG2RAD;
            double sun_mean_anomaly_rad = sun_mean_anomaly_deg * DEG2RAD;
            double moon_mean_anomaly_rad = moon_mean_anomaly_deg * DEG2RAD;
            double moon_argument_of_latitude_rad = moon_argument_of_latitude_deg * DEG2RAD;

            double geocentric_ecliptic_longitude_deg = moon_mean_longitude_deg
                + 6.2888 * Math.sin (moon_mean_anomaly_rad)
                + 1.2740 * Math.sin (2 * mean_elongation_rad - moon_mean_anomaly_rad)
                + 0.6583 * Math.sin (2 * mean_elongation_rad)
                + 0.2136 * Math.sin (2 * mean_elongation_rad - sun_mean_anomaly_rad)
                - 0.1856 * Math.sin (sun_mean_anomaly_rad)
                - 0.1143 * Math.sin (2 * moon_argument_of_latitude_rad)
                - 0.0588 * Math.sin (2 * mean_elongation_rad - 2 * moon_mean_anomaly_rad)
                + 0.0572 * Math.sin (2 * mean_elongation_rad - sun_mean_anomaly_rad - moon_mean_anomaly_rad)
                + 0.0533 * Math.sin (2 * mean_elongation_rad + moon_mean_anomaly_rad);

            double geocentric_ecliptic_latitude_deg = 5.1282 * Math.sin (moon_argument_of_latitude_rad)
                + 0.2806 * Math.sin (moon_mean_anomaly_rad + moon_argument_of_latitude_rad)
                + 0.2777 * Math.sin (moon_mean_anomaly_rad - moon_argument_of_latitude_rad)
                + 0.1732 * Math.sin (2 * mean_elongation_rad - moon_argument_of_latitude_rad);

            double geocentric_dist_km = 385000.6
                - 20905.0 * Math.cos (moon_mean_anomaly_rad)
                - 3699.0 * Math.cos (2 * mean_elongation_rad - moon_mean_anomaly_rad)
                - 2956.0 * Math.cos (2 * mean_elongation_rad)
                - 570.0 * Math.cos (2 * moon_mean_anomaly_rad)
                + 246.0 * Math.cos (2 * mean_elongation_rad - 2 * moon_mean_anomaly_rad)
                - 205.0 * Math.cos (2 * mean_elongation_rad - sun_mean_anomaly_rad)
                - 171.0 * Math.cos (2 * mean_elongation_rad + moon_mean_anomaly_rad)
                - 152.0 * Math.cos (2 * mean_elongation_rad - sun_mean_anomaly_rad - moon_mean_anomaly_rad);

            double parallax_sin = 6378.137 / geocentric_dist_km;

            double sun_mean_longitude = 280.46646 + 36000.76983 * centuries_since_j2000 + 0.0003032 * centuries_since_j2000_sq;
            sun_mean_longitude = Math.fmod (sun_mean_longitude, 360.0);
            if (sun_mean_longitude < 0) sun_mean_longitude += 360.0;

            double sun_eq_center = sun_eq_c1 * Math.sin (sun_mean_anomaly_rad)
                + sun_eq_c2 * Math.sin (2 * sun_mean_anomaly_rad)
                + 0.000289 * Math.sin (3 * sun_mean_anomaly_rad);

            double sun_true_longitude = sun_mean_longitude + sun_eq_center;

            double omega = moon_mean_longitude_deg - moon_argument_of_latitude_deg;
            double sun_apparent_longitude = sun_true_longitude - 0.00569 - 0.00478 * Math.sin (omega * DEG2RAD);

            double lambda_moon_rad = geocentric_ecliptic_longitude_deg * DEG2RAD;
            double beta_moon_rad = geocentric_ecliptic_latitude_deg * DEG2RAD;
            double lambda_sun_rad = sun_apparent_longitude * DEG2RAD;

            double cos_elongation = Math.cos (beta_moon_rad) * Math.cos (lambda_moon_rad - lambda_sun_rad);

            double illuminated_fraction = (1.0 - cos_elongation) / 2.0;

            double diff_long = geocentric_ecliptic_longitude_deg - sun_apparent_longitude;
            diff_long = Math.fmod (diff_long, 360.0);
            if (diff_long < 0) diff_long += 360.0;

            moon_phases[i] = illuminated_fraction;
            moon_elongations[i] = diff_long;

            double geocentric_ecliptic_longitude_rad = geocentric_ecliptic_longitude_deg * DEG2RAD;
            double geocentric_ecliptic_latitude_rad = geocentric_ecliptic_latitude_deg * DEG2RAD;

            double sin_ecl_lon = Math.sin (geocentric_ecliptic_longitude_rad);
            double cos_ecl_lon = Math.cos (geocentric_ecliptic_longitude_rad);
            double sin_ecl_lat = Math.sin (geocentric_ecliptic_latitude_rad);
            double cos_ecl_lat = Math.cos (geocentric_ecliptic_latitude_rad);

            double ra_sin_component = sin_ecl_lon * obliquity_cos - Math.tan (geocentric_ecliptic_latitude_rad) * obliquity_sin;
            double ra_cos_component = cos_ecl_lon;
            double geocentric_ra_rad = Math.atan2 (ra_sin_component, ra_cos_component);

            double geocentric_dec_sin = sin_ecl_lat * obliquity_cos + cos_ecl_lat * obliquity_sin * sin_ecl_lon;
            double geocentric_dec_rad = Math.asin (geocentric_dec_sin);

            double greenwich_mean_sidereal_time_deg = 280.46061837 + 360.98564736629 * local_days_since_j2000;
            greenwich_mean_sidereal_time_deg = Math.fmod (greenwich_mean_sidereal_time_deg, 360.0);
            if (greenwich_mean_sidereal_time_deg < 0) greenwich_mean_sidereal_time_deg += 360.0;

            double local_mean_sidereal_time_deg = greenwich_mean_sidereal_time_deg + longitude_deg;
            double local_mean_sidereal_time_rad = local_mean_sidereal_time_deg * DEG2RAD;

            double hour_angle_rad = local_mean_sidereal_time_rad - geocentric_ra_rad;

            double declination_cos = Math.cos (geocentric_dec_rad);

            double sin_hour_angle = Math.sin (hour_angle_rad);
            double cos_hour_angle = Math.cos (hour_angle_rad);

            double a_component = declination_cos * sin_hour_angle;
            double a_sq = a_component * a_component;
            double b_component = declination_cos * cos_hour_angle - rho_cos_phi_prime * parallax_sin;
            double b_sq = b_component * b_component;
            double c_component = geocentric_dec_sin - rho_sin_phi_prime * parallax_sin;
            double c_sq = c_component * c_component;

            double topocentric_hour_angle_rad = Math.atan2 (a_component, b_component);
            double topocentric_horizontal_distance = Math.sqrt (a_sq + b_sq);
            double topocentric_declination_rad = Math.atan2 (c_component, topocentric_horizontal_distance);

            double elevation_sin = sin_lat * Math.sin (topocentric_declination_rad)
                + cos_lat * Math.cos (topocentric_declination_rad) * Math.cos (topocentric_hour_angle_rad);

            double true_elevation_deg = Math.asin (elevation_sin.clamp (-1.0, 1.0)) * RAD2DEG;
            moon_angles[i] = true_elevation_deg + calculate_refraction (true_elevation_deg, refraction_factor);

            double dist_ratio = Math.sqrt (a_sq + b_sq + c_sq);
            moon_distances[i] = dist_ratio * geocentric_dist_km;
        }
    }

    /**
     * Updates lunar angle data for current settings.
     */
    private void update_plot_data () {
        double latitude_rad = latitude * DEG2RAD;
        // Convert DateTime to Date and get Julian Day Number
        var date = Date ();
        date.set_dmy ((DateDay) selected_date.get_day_of_month (),
                      selected_date.get_month (),
                      (DateYear) selected_date.get_year ());
        var julian_date = (double) date.get_julian ();
        generate_moon_angles (latitude_rad, longitude, timezone_offset_hours, julian_date);
        has_click_point = false;
        click_info_label.label = DEFAULT_INFO_LABEL;
    }

    /**
     * Calculates atmospheric refraction using Saemundsson's formula.
     *
     * The formula R = 1.02 / tan(h + 10.3/(h+5.11)) mathematically fails
     * when the inner argument exceeds 90 degrees or creates a singularity.
     * The roots are exactly ~ -5.0015 and ~ 89.8915.
     * Inside this range, the formula is valid.
     *
     * @param true_elevation_deg True elevation angle in degrees.
     * @param refraction_factor Factor to scale the refraction effect.
     */
    private static double calculate_refraction (double true_elevation_deg, double refraction_factor) {
        if (refraction_factor == 0.0) {
            return 0.0;
        }
        if (true_elevation_deg > 89.8915 || true_elevation_deg < -5.0015) {
            return 0.0;
        }

        double angle_arg = (true_elevation_deg + 10.3 / (true_elevation_deg + 5.11)) * DEG2RAD;
        return 1.02 / 60.0 / Math.tan (angle_arg) * refraction_factor;
    }

    /**
     * Handles mouse click events on the chart.
     *
     * @param n_press Number of button presses.
     * @param x X coordinate of the click.
     * @param y Y coordinate of the click.
     */
    private void on_chart_clicked (int n_press, double x, double y) {
        int width = drawing_area.get_width ();
        int height = drawing_area.get_height ();
        int chart_width = width - MARGIN_LEFT - MARGIN_RIGHT;

        if (x >= MARGIN_LEFT && x <= width - MARGIN_RIGHT && y >= MARGIN_TOP && y <= height - MARGIN_BOTTOM && n_press == 1) {
            clicked_time_hours = (x - MARGIN_LEFT) / chart_width * 24.0;
            int time_minutes = (int) (clicked_time_hours * 60);
            corresponding_angle = moon_angles[time_minutes];
            double phase = moon_phases[time_minutes];
            double elongation = moon_elongations[time_minutes];
            has_click_point = true;

            int hours = (int) clicked_time_hours;
            int minutes = (int) ((clicked_time_hours - hours) * 60);

            string info_text = "Time: %02d:%02d\nElevation: %.1f°\nDistance: %.0f km\nPhase: %s".printf (
                hours, minutes, corresponding_angle, moon_distances[time_minutes], get_phase_description (phase, elongation)
            );
            click_info_label.label = info_text;
            drawing_area.queue_draw ();
        } else {
            has_click_point = false;
            click_info_label.label = DEFAULT_INFO_LABEL;
            drawing_area.queue_draw ();
        }
    }

    /**
     * Draws the lunar elevation chart.
     *
     * @param area The drawing area widget.
     * @param cr The Cairo context for drawing.
     * @param width The width of the drawing area.
     * @param height The height of the drawing area.
     */
    private void draw_lunar_angle_chart (Gtk.DrawingArea area, Cairo.Context cr, int width, int height) {
        ThemeColors colors = style_manager.dark ? DARK_THEME : LIGHT_THEME;

        cr.set_source_rgb (colors.bg_r, colors.bg_g, colors.bg_b);
        cr.paint ();

        int chart_width = width - MARGIN_LEFT - MARGIN_RIGHT;
        int chart_height = height - MARGIN_TOP - MARGIN_BOTTOM;
        double horizon_y = MARGIN_TOP + chart_height * 0.5;

        // Shade area below horizon
        cr.set_source_rgba (colors.shade_r, colors.shade_g, colors.shade_b, colors.shade_a);
        cr.rectangle (MARGIN_LEFT, horizon_y, chart_width, height - MARGIN_BOTTOM - horizon_y);
        cr.fill ();

        // Grid
        cr.set_source_rgba (colors.grid_r, colors.grid_g, colors.grid_b, colors.grid_a);
        cr.set_line_width (1);
        for (int angle = -90; angle <= 90; angle += 15) {
            double tick_y = MARGIN_TOP + chart_height * (90 - angle) / 180.0;
            cr.move_to (MARGIN_LEFT, tick_y);
            cr.line_to (width - MARGIN_RIGHT, tick_y);
            cr.stroke ();
        }
        for (int h = 0; h <= 24; h += 2) {
            double tick_x = MARGIN_LEFT + chart_width * (h / 24.0);
            cr.move_to (tick_x, MARGIN_TOP);
            cr.line_to (tick_x, height - MARGIN_BOTTOM);
            cr.stroke ();
        }

        // Axes
        cr.set_source_rgb (colors.axis_r, colors.axis_g, colors.axis_b);
        cr.set_line_width (2);
        cr.move_to (MARGIN_LEFT, height - MARGIN_BOTTOM);
        cr.line_to (width - MARGIN_RIGHT, height - MARGIN_BOTTOM);
        cr.stroke ();
        cr.move_to (MARGIN_LEFT, MARGIN_TOP);
        cr.line_to (MARGIN_LEFT, height - MARGIN_BOTTOM);
        cr.stroke ();
        cr.move_to (MARGIN_LEFT, horizon_y);
        cr.line_to (width - MARGIN_RIGHT, horizon_y);
        cr.stroke ();

        // Labels
        cr.set_source_rgb (colors.text_r, colors.text_g, colors.text_b);
        cr.set_line_width (1);
        cr.set_font_size (20);
        for (int angle = -90; angle <= 90; angle += 15) {
            double tick_y = MARGIN_TOP + chart_height * (90 - angle) / 180.0;
            cr.move_to (MARGIN_LEFT - 5, tick_y);
            cr.line_to (MARGIN_LEFT, tick_y);
            cr.stroke ();
            var txt = angle.to_string ();
            Cairo.TextExtents te;
            cr.text_extents (txt, out te);
            cr.move_to (MARGIN_LEFT - 10 - te.width, tick_y + te.height / 2);
            cr.show_text (txt);
        }
        for (int h = 0; h <= 24; h += 2) {
            double tick_x = MARGIN_LEFT + chart_width * (h / 24.0);
            cr.move_to (tick_x, height - MARGIN_BOTTOM);
            cr.line_to (tick_x, height - MARGIN_BOTTOM + 5);
            cr.stroke ();
            var txt = h.to_string ();
            Cairo.TextExtents te;
            cr.text_extents (txt, out te);
            cr.move_to (tick_x - te.width / 2, height - MARGIN_BOTTOM + 25);
            cr.show_text (txt);
        }

        // Curve
        cr.set_source_rgb (colors.curve_r, colors.curve_g, colors.curve_b);
        cr.set_line_width (2);
        for (int i = 0; i < RESOLUTION_PER_MIN; i += 1) {
            double x = MARGIN_LEFT + chart_width * (i / (double) (RESOLUTION_PER_MIN - 1));
            double y = MARGIN_TOP + chart_height * (90.0 - moon_angles[i]) / 180.0;
            if (i == 0) cr.move_to (x, y);
            else cr.line_to (x, y);
        }
        cr.stroke ();

        // Click point
        if (has_click_point) {
            double clicked_x = MARGIN_LEFT + chart_width * (clicked_time_hours / 24.0);
            double corresponding_y = MARGIN_TOP + chart_height * (90.0 - corresponding_angle) / 180.0;

            cr.set_source_rgba (colors.point_r, colors.point_g, colors.point_b, 0.8);
            cr.arc (clicked_x, corresponding_y, 5, 0, 2 * Math.PI);
            cr.fill ();

            cr.set_source_rgba (colors.line_r, colors.line_g, colors.line_b, colors.line_a);
            cr.set_line_width (1);
            cr.move_to (clicked_x, MARGIN_TOP);
            cr.line_to (clicked_x, height - MARGIN_BOTTOM);
            cr.stroke ();
            cr.move_to (MARGIN_LEFT, corresponding_y);
            cr.line_to (width - MARGIN_RIGHT, corresponding_y);
            cr.stroke ();
        }

        // Titles
        cr.set_source_rgb (colors.text_r, colors.text_g, colors.text_b);
        cr.set_font_size (20);
        string x_title = "Time (hours)";
        Cairo.TextExtents x_ext;
        cr.text_extents (x_title, out x_ext);
        cr.move_to ((double) width / 2 - x_ext.width / 2, height - MARGIN_BOTTOM + 55);
        cr.show_text (x_title);

        string y_title = "Lunar Elevation (°)";
        Cairo.TextExtents y_ext;
        cr.text_extents (y_title, out y_ext);
        cr.save ();
        cr.translate (MARGIN_LEFT - 45, (double)height / 2);
        cr.rotate (-Math.PI / 2);
        cr.move_to (-y_ext.width / 2, 0);
        cr.show_text (y_title);
        cr.restore ();

        // Captions
        string caption_line1 = "Lunar Elevation Angle - Date: %s".printf (selected_date.format ("%Y-%m-%d"));
        string caption_line2 = "Lat: %.2f°, Lon: %.2f°, TZ: UTC%+.2f".printf (latitude, longitude, timezone_offset_hours);

        cr.set_font_size (18);
        Cairo.TextExtents cap_ext1, cap_ext2;
        cr.text_extents (caption_line1, out cap_ext1);
        cr.text_extents (caption_line2, out cap_ext2);

        double total_caption_height = cap_ext1.height + cap_ext2.height + 5;
        cr.move_to ((width - cap_ext1.width) / 2, (MARGIN_TOP - total_caption_height) / 2 + cap_ext1.height);
        cr.show_text (caption_line1);
        cr.move_to ((width - cap_ext2.width) / 2, (MARGIN_TOP - total_caption_height) / 2 + cap_ext1.height + 5 + cap_ext2.height);
        cr.show_text (caption_line2);
    }

    /**
     * Handles export button click event.
     *
     * Shows a file save dialog with filters for PNG, SVG, and PDF formats.
     */
    private void on_export_clicked () {
        var png_filter = new Gtk.FileFilter (); png_filter.name = "PNG Images"; png_filter.add_mime_type ("image/png");
        var svg_filter = new Gtk.FileFilter (); svg_filter.name = "SVG Images"; svg_filter.add_mime_type ("image/svg+xml");
        var pdf_filter = new Gtk.FileFilter (); pdf_filter.name = "PDF Documents"; pdf_filter.add_mime_type ("application/pdf");

        var filter_list = new ListStore (typeof (Gtk.FileFilter));
        filter_list.append (png_filter); filter_list.append (svg_filter); filter_list.append (pdf_filter);

        var file_dialog = new Gtk.FileDialog () {
            modal = true,
            initial_name = "lunar_elevation_chart.png",
            filters = filter_list,
        };
        file_dialog.save.begin (window, null, (obj, res) => {
            try {
                var file = file_dialog.save.end (res);
                if (file != null) export_chart (file);
            } catch (Error e) {
                message ("Image file has not been saved: %s", e.message);
            }
        });
    }

    /**
     * Exports the current chart to a file.
     *
     * Supports PNG, SVG, and PDF formats based on file extension.
     * Defaults to PNG if extension is not recognized.
     *
     * @param file The file to export the chart to.
     */
    private void export_chart (File file) {
        int width = drawing_area.get_width ();
        int height = drawing_area.get_height ();
        if (width <= 0) { width = 800; height = 600; }

        string filepath = file.get_path ();
        string? extension = null;
        var last_dot = filepath.last_index_of_char ('.');
        if (last_dot != -1) extension = filepath[last_dot:].down ();

        if (extension == ".svg") {
            var surface = new Cairo.SvgSurface (filepath, width, height);
            var cr = new Cairo.Context (surface);
            draw_lunar_angle_chart (drawing_area, cr, width, height);
        } else if (extension == ".pdf") {
            var surface = new Cairo.PdfSurface (filepath, width, height);
            var cr = new Cairo.Context (surface);
            draw_lunar_angle_chart (drawing_area, cr, width, height);
        } else {
            var surface = new Cairo.ImageSurface (Cairo.Format.RGB24, width, height);
            var cr = new Cairo.Context (surface);
            draw_lunar_angle_chart (drawing_area, cr, width, height);
            surface.write_to_png (filepath);
        }
    }

    /**
     * Handles CSV export button click event.
     *
     * Shows a file save dialog for CSV format.
     */
    private void on_export_csv_clicked () {
        var csv_filter = new Gtk.FileFilter ();
        csv_filter.name = "CSV Files";
        csv_filter.add_mime_type ("text/csv");
        var filter_list = new ListStore (typeof (Gtk.FileFilter));
        filter_list.append (csv_filter);
        var file_dialog = new Gtk.FileDialog () {
            modal = true,
            initial_name = "lunar_elevation_data.csv",
            filters = filter_list,
        };
        file_dialog.save.begin (window, null, (obj, res) => {
            try {
                var file = file_dialog.save.end (res);
                if (file != null) export_csv_data (file);
            } catch (Error e) {
                message ("CSV file has not been saved: %s", e.message);
            }
        });
    }

    /**
     * Exports the lunar data to a CSV file.
     *
     * @param file The file to export the data to.
     */
    private void export_csv_data (File file) {
        try {
            var stream = file.replace (null, false, FileCreateFlags.REPLACE_DESTINATION);
            var data_stream = new DataOutputStream (stream);

            data_stream.put_string ("# Lunar Data\n");
            data_stream.put_string ("# Date: %s\n".printf (selected_date.format ("%Y-%m-%d")));
            data_stream.put_string ("# Latitude: %.2f, Longitude: %.2f\n".printf (latitude, longitude));
            data_stream.put_string ("# Timezone: UTC%+.2f\n".printf (timezone_offset_hours));
            data_stream.put_string ("#\n");
            data_stream.put_string ("Time,Elevation(deg),Illumination,Distance(km)\n");

            for (int i = 0; i < RESOLUTION_PER_MIN; i += 1) {
                int hours = i / 60;
                int minutes = i % 60;
                data_stream.put_string (
                    "%02d:%02d,%.3f,%.2f%%,%.0f\n".printf (hours, minutes, moon_angles[i], moon_phases[i] * 100.0, moon_distances[i])
                );
            }
            data_stream.close ();
        } catch (Error e) {
            show_error_dialog ("CSV export failed", e.message);
        }
    }

    /**
     * Application entry point.
     *
     * Creates and runs the LunarCalc instance.
     *
     * @param args Command line arguments.
     * @return Exit code.
     */
    public static int main (string[] args) {
        var app = new LunarCalc ();
        return app.run (args);
    }
}

本文采用CC-BY-SA-4.0协议发布，但本文代码采用LGPL v2.1+协议公开。本文各示意图如无特殊说明均由作者自行绘制，亦采用CC-BY-SA-4.0协议。 ↩

探索月球运动的复杂性——计算月球位置与相位的 Vala 实现

前言