本文主要由我参与Wikipedia条目:应变 (化学) 的时候作的一些草稿整理而来。该条目在我编辑之前语序混乱,结构颠倒,内容缺失,且有非常多的知识性错误,应该是在2013年由一位不太了解化学的台湾朋友使用当时拙劣的机翻技术创建的。由于原文表述过于混乱,编辑改进十分困难,故我将在本文中持续更新我的编辑过程,很多编辑中力不从心的地方也欢迎读者提供建议。
- 2022.01.29更新:我的维基百科IP封禁豁免权过期了,现在不能编辑,等管理员再次审核通过不知道要等多久……
本文可能得暂时搁置一下了 - 2022.01.30更新:IP封禁豁免权现在已经回来了,继续~~~
- 2022.02.06更新:主体差不多完成了……剩下的工作以后再做😜😜😜😜😜😜
分子应变的概念
在化学中,分子在受到应力作用时会产生应变。应变会使得分子的结构更加不稳定,令分子的内能更高。应变令分子额外增加的内能称为应变能,1 正如压缩后的弹簧可以受固定而防止势能释放,分子也可以通过该分子内的键合作用保持在热力学不稳定的构像上。 如果没有可以将构象保持在适当位置的键,应变能就会释放出来。
摘要
热力学
由吉布斯自由能差值可确定两构象异构体间相互转化的平衡常数。
若分子的状态转变过程伴随吉布斯自由能降低,则此转变是自发反应。因此,高能量的构象会自发变成较低能量的构象。
焓和熵与吉布斯自由能在恒温下满足以下方程:
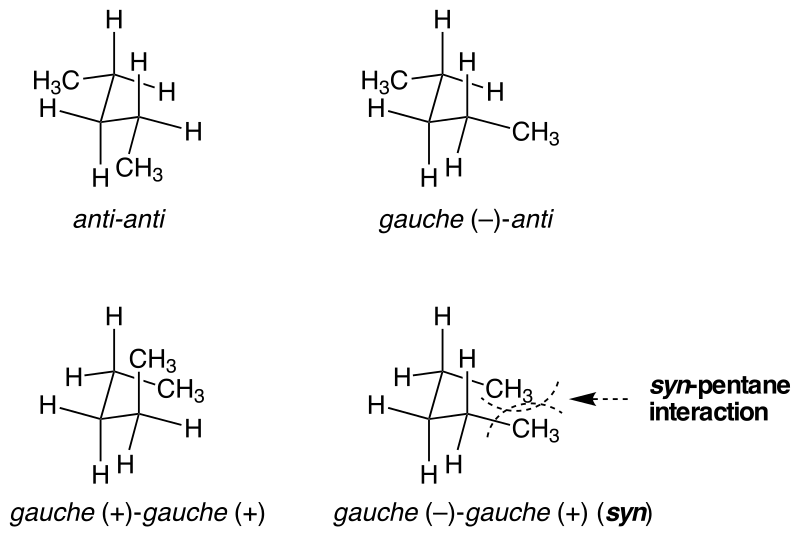
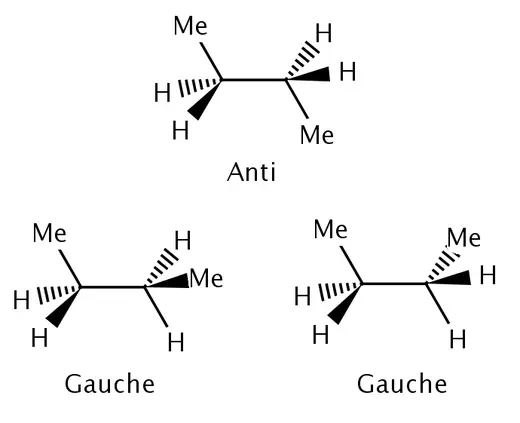
焓在热力学中常用来确定更稳定的分子构象。1应变能是由于分子内键强度减弱所致。 所以通常焓影响较大,起主导作用,而熵可以忽略。1但是,当焓的值较小时,熵则不可忽略。例如,丁烷有对交叉构象与邻交叉构象。对交叉构象比邻交叉构象稳定0.9 kcal/mol(3.8 kJ/mol)。1由此可以计算出在室温下丁烷有约82%采用对交叉构象,18%采用邻交叉构象。但是邻交叉构象又有两种可能,而对扭构象则直有一种可能。所以熵在邻交叉构象中提供0.4 kcal/mol(1.7 kJ/mol) 的能量。2实验表明,丁烷在室温下有70%为对交叉构象,30%为邻交叉构象,这可以说明在焓变较小的情况下,熵是不能忽略的。
 |
|---|
| 例子:丁烷的对交叉构象(anti)和邻交叉构象(gauche) |
确定分子的应变能
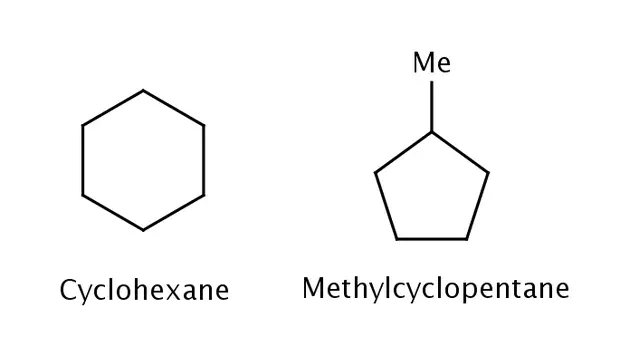
标准摩尔生成焓 (ΔHfo)指在标准状态(101.3 kPa;25 ℃)下,生成1摩尔纯净物质放出(符号为负)或者吸收(符号为正)的热量。3在应变能的影响下,化合物的生成焓和预测值可能会有一定差异。例如,环己烷的生成焓 ΔHfo 为-29.9 kcal/mol(-125 kJ/mol),而甲基环戊烷的生成焓 ΔHfo 为-25.5 kcal/mol(-107 kJ/mol)。1环己烷和甲基环戊烷有着一样的分子式和键数,由于两者受到的环张力不同,它们的生成焓却存在一定差异。在相关能量的实验上,通常会使用方便实验测定与计算使用的燃烧焓。
 |
|---|
| 环己烷和甲基环戊烷 |
计算出应变能需要了解化合物在无应变情况下的能量状况。有两种可用于确定的方式。 第一种是将该化合物的燃烧焓或其他能量数据与结构类似但不受应变影响的参考化合物相比(例如前面甲基环戊烷的例子),但是,寻找合适的参考化合物通常较为困难。第二种方式是利用Benson基团增量理论,增加或延长化合物上的部分基团(如引入新的烷基或是利用取代反应改变分子结构)可以得到一种新的化合物,由经验进行加和计算可以估计出新化合物的燃烧焓。而燃烧焓估计值和实验值的能量差主要由应变造成,由此即可估计分子应变能的大小。
应变能的类型
范德华斥力
范德华斥力(或立体张力、凡得瓦张力、范氏张力),是未键合的原子因分子的立体构型要求而被迫靠近,使得两原子的间距小于两者范德华半径而产生的排斥力。范德华斥力模型中互相作用的原子或基团之间彼此间隔四个键。4基团的大小是影响范德华斥力的重要因素,体积庞大的叔丁基进的范德华斥力比甲基大得多。
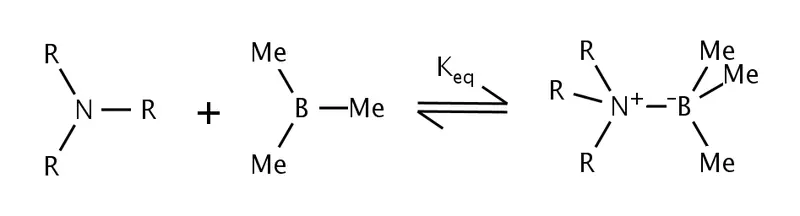
Brown 等人进行了关于三烷基胺和三甲基硼加合物立体张力的研究。5他们发现当三烷基胺的烷基链大小增加时,加合反应平衡常数就会下降。利用三烷基胺和三甲基硼之间甲基基团的立体张力可以计算不同基团造成的立体张力的差异。
 |
|---|
| 三烷基胺和三甲基硼形成的加合物中存在范德华斥力 |
邻交叉(-)-邻交叉(+)-戊烷张力
戊烷的两种邻交叉-邻交叉式构象能量有所不同,邻交叉(-)-邻交叉(+)式构象的能量比邻交叉(+)-邻交叉(+)式构象高约3 kcal/mol(13 kJ/mol)。1 邻交叉(-)-邻交叉(+)式构象中形成了类似环戊烷的结构,在此结构中,分子两端的甲基靠得很近,斥力大。而另一个构象中则不存在这种空间效应。
对于其他类似的分子,当分子中的部分结构采取邻交叉(-)-邻交叉(+)构象时,也易使得结构两端体积较大的基团过于靠近而令分子的能量升高,产生应变能,降低分子的稳定性。
烯丙基斥力
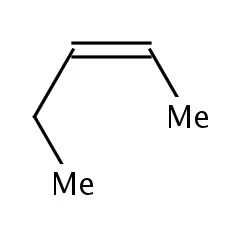
烯丙基张力(或A1,3张力)与邻交叉(-)-邻交叉(+)-戊烷张力的基本模型较为相似。例如2-戊烯的乙基取代基在如图所示的构象中与另一端的甲基均朝向分子内侧,十分靠近,有较为明显的斥力。因此,这类物质倾向于采取折线形的构象以避免基团间产生烯丙基张力。
 |
|---|
| 烯丙基甲基和乙基基团在此构象中相当接近 |
1,3-二直键张力
1,3-二直键张力与邻交叉(-)-邻交叉(+)-戊烷张力类似。这种张力主要因环己烷直键位置上的取代基间空间距离接近,发生相互作用而产生。此外,直键取代基与相邻的两个亚甲基之间的扭转张力对此也有一定的贡献(但此张力在平伏键仍然存在)。1,3-二直键张力的应变能很大程度上取决于取代基的空间大小。
对于一个给定的环己烷取代基,由于1,3-二直键张力的存在,其处于直立键的构象的能量与处于平伏键时的构象能量不同。这两个构象间的能量差称为A值。A值可以通过热力学方法测得。例如,利用Meerwein-Ponndorf-Verley还原和Oppenauer氧化之间的平衡可以测定环己醇的A值。
扭转张力
扭转张力是对抗键旋转所产生的张力。
当间隔三个键的原子处于重叠式时,由于重叠式构象不稳定,会产生扭转张力。例如,乙烷的重叠式构象比交叉式构象能量高2.9 kcal/mol(12 kJ/mol)。1
以前的主流观点认为,重叠式能量较高是因为沿C-C键方向投影相重合的各对氢原子之间存在着范德华斥力。但是对于乙烷来说,氢的范德华半径很小,这种斥力并不明显。最近的研究表明,乙烷采取交叉式构象的主要原因是交叉式构象存在超共轭效应。6
较复杂的分子可能有多种交叉式构象,这些交叉式构象间的能量往往不同。如,对交叉构象的丁烷比邻交叉构象的丁烷稳定3.8 kcal/mol(16 kJ/mol)。1
环张力
根据价层电子对互斥理论,在稳定的分子结构中,电子对间应当尽量远离,互相保持在一个最优的角度。但是,在实际分子中,键角大小常常会偏离理想值。这种应变称为角张力或Baeyer应变。7 对于角张力,最简单的例子是小环烷烃,如环丙烷、环丁烷。下表示出了一些环烷烃的应变能。
| 环的大小 | 张力能(kcal/mol) | 张力能(kJ/mol) |
|---|---|---|
| 3 | 27.5 | 115 |
| 4 | 26.3 | 110 |
| 5 | 6.2 | 26.0 |
| 6 | 0.1 | 0.4 |
| 7 | 6.2 | 26.0 |
| 8 | 9.7 | 40.6 |
| 9 | 12.6 | 52.7 |
| 10 | 12.4 | 51.9 |
| 11 | 11.3 | 47.3 |
| 12 | 4.1 | 17.2 |
| 13 | 5.2 | 21.8 |
| 14 | 1.9 | 7.95 |
| 15 | 1.9 | 7.95 |
| 16 | 2.0 | 8.37 |
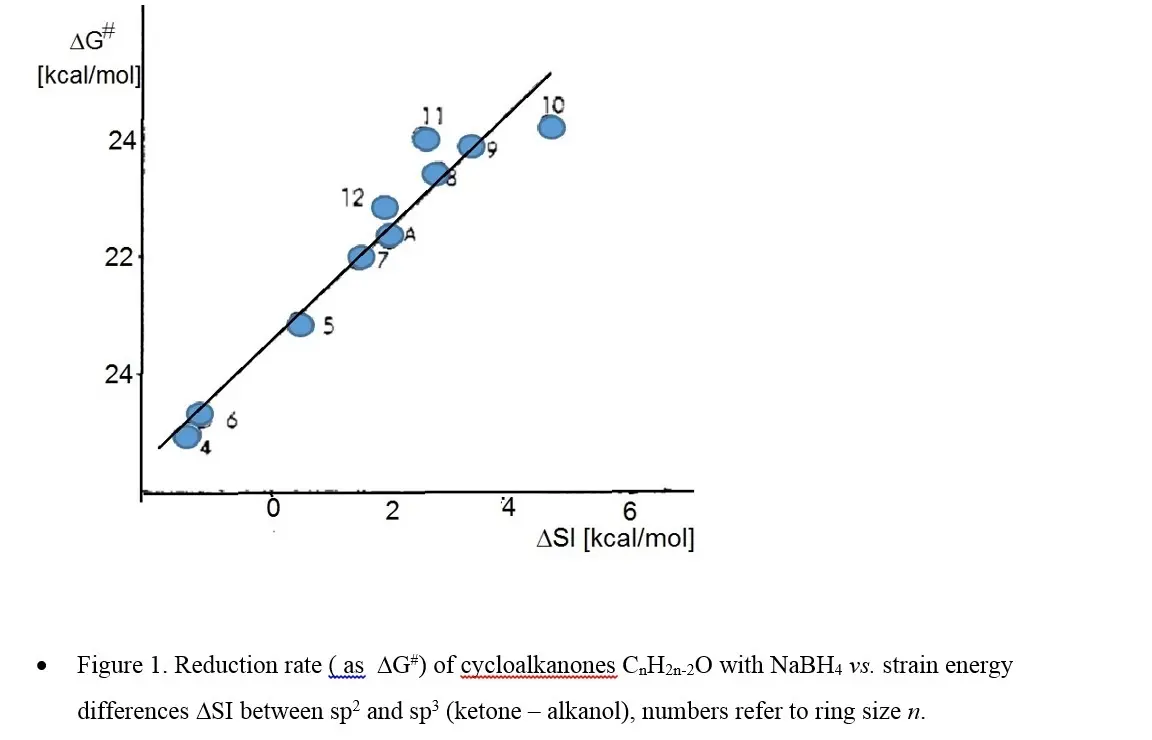
此外,在环状分子中,常常还会有皮策应变。H.C. Brown曾将这些张力和跨环张力总结为内部张力。脂环化合物有许多涉及原子杂化方式的转变(一般是sp2与sp3间相互转化)的反应,这些反应的倾向往往会与相应结构的应变能差相关。例如,随着sp2与sp3对于分子的应变能差增加,酮的还原率明显增加(图1 B)。
 |
|---|
| 图1 B |
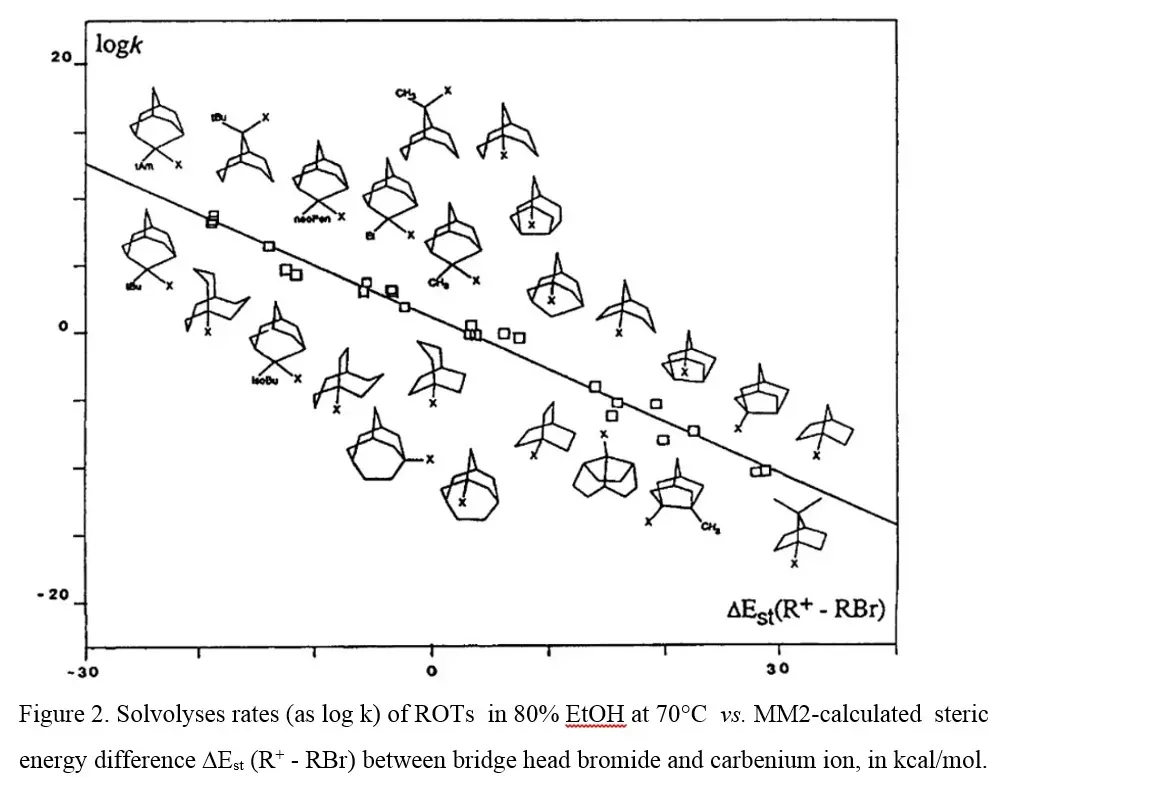
另一个例子是桥头甲苯磺酸酯的溶剂解,该过程显著受桥头碳sp2与sp3的应变能差影响(图2 B)。
 |
|---|
| 图2 B |
小环张力
环己烷几乎没有应变能,因此,常将其作为确定环烷烃有无环张力的基准。1 一般来说,小环烷烃通常具有较大的应变能。例如,在环丙烷中,C-C键间的键角为60°,远低于sp3杂化的理想角度109.5°;此外,环丙烷中的氢为重叠式构象。这些因素使得环丙烷的应变能极大。与环丙烷类似,环丁烷也有很大的应变能,因为它的C-C键间键角仅有88°,且氢原子间也接近重叠式构象。环丙烷和环丁烷的应变能分别高达27.5 kcal/mol(115 kJ/mol)和26.3 kcal/mol(110 kJ/mol)。1 相比前两者,环戊烷的键角压缩程度有较大疏解,且分子内部发生了键扭转,减少了重叠式氢之间的斥力,因此,环戊烷的张力较小,应变能仅6.2 kcal/mol(26 kJ/mol)。
中环张力
由于具有明显的扭转张力,中环(7-13元环)的应变能比大环更大。虽然中环体系中容易发生1,5-迁移反应可能表明中环体系内的跨环位点十分接近,这也意味着分子内可能存在较大的跨环斥力,但分子力学计算表明,跨环斥力并不是中环张力的主要贡献因素。
双环张力
双环系统中的应变能通常是每个环中应变能的总和。1 但是,有时候环系间相结合还会引入额外的张力。
参考文献
本文采用CC-BY-SA-4.0协议发布,来自我参与编辑的Wikipedia条目应变 (化学),由于个人水平限制,本条目难免会有知识谬误以及描述不清等情况,欢迎读者在维基条目中编辑修改或对本网站在GitHub上的源代码提供Pull request,也欢迎在评论区多多指教。
-
Anslyn and Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006, ISBN 978-1-891389-31-3 ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7 ↩8 ↩9 ↩10 ↩11
-
Coxon and Norman, Principles of Organic Synthesis, 3rd ed., Blackie Academic & Pro., 1993, ISBN 978-0-7514-0126-4 ↩
-
Levine, Physical Chemistry, 5th ed., McGraw-Hill, 2002, ISBN 978-0-07-253495-5 ↩
-
Brown, Foote, and Iverson, Organic Chemistry, 4th ed., Brooks/Cole, 2005, ISBN 978-0-534-46773-9 ↩
-
Brown, Herbert C.; Johannesen, Rolf B. Dissociation of the Addition Compounds of Trimethylboron with n-Butyl- and Neopentyldimethylamines; Interaction of Trimethylboron and Boron Trifluoride with Highly Hindered Bases 1,2. Journal of the American Chemical Society. 1953-01, 75 (1): 16–20. ISSN 0002-7863. doi:10.1021/ja01097a005 (英语). ↩
-
Weinhold, Frank. A new twist on molecular shape. Nature. 2001-05, 411 (6837): 539–541. ISSN 0028-0836. PMID 11385553. doi:10.1038/35079225 (英语). ↩
-
Wiberg, Kenneth B. The Concept of Strain in Organic Chemistry. Angewandte Chemie International Edition in English. 1986-04, 25 (4): 312–322. ISSN 0570-0833. doi:10.1002/anie.198603121 (英语). ↩