前言
Vala 语言以其将高级语言的便利性与C语言的原始性能相结合的特点,在桌面应用开发领域(尤其是 GNOME 生态)备受青睐。然而,它的能力远不止于构建用户界面。Vala 编译到C的本质,使其在需要高性能的数值与科学计算场景中,同样是一个值得考虑的强大选项。
本文旨在探讨 Vala 在科学计算领域的应用潜力。我们将以一个经典的天文学问题——精确计算太阳在天空中的位置——作为核心案例,从零开始,分步详解如何用 Vala 实现国际上广受认可的 Meeus 算法。
我们将看到,Vala 不仅能胜任复杂的数学运算,其现代化的语言特性、清晰的面向对象结构以及与 GLib 等底层库的无缝集成,都能让我们的科学计算代码变得既高效又易于维护。
这篇文章的算法实现,被用于笔者在上一篇教程中介绍的 GTK4 太阳高度角计算器 中,但本文的重点并非 GUI 应用本身,而是算法的理论、实现细节及其在 Vala 语言中的最佳实践。
算法背景:为何选择 Meeus 算法?
计算太阳位置存在不同层次的解法,复杂度与精度各不相同:
- 经验公式:例如一些基于傅里叶级数拟合的简化模型(如 Spencer 的算法)。这类公式易于实现,对于一般性应用(如常规的日照模拟)精度足够,但它们是观测数据的近似,缺乏坚实的物理基础。
- 高精度天文历:由专业天文机构(如 NASA JPL)发布的星历表,如 DE430、DE440 等。它们提供了最精确的行星位置数据,但通常体积庞大,使用和解析也相对复杂。
- 解析理论(Analytical Theory):介于两者之间,基于天体力学模型,但通过一系列数学简化,得到一组可以直接计算的解析公式。Meeus 算法正是此类方法的杰出代表,它由比利时气象学家兼天文学家 Jean Meeus 在其著作《天文算法》(Astronomical Algorithms)中推广,能在不依赖大型星历表的情况下,达到非常高的精度(通常优于 1 角分),是业余天文学和许多科学应用中的“黄金标准”。
本文选择 Meeus 算法,旨在展示如何在 Vala 中处理一个兼具理论深度和实现复杂度的真实科学计算问题。
Meeus 算法的 Vala 实现:分步详解
为了便于在代码中直接使用以“天”为单位的儒略日,笔者对原始公式进行了一定的恒等变形。原始公式通常基于儒略世纪数(Julian Centuries, $T$)作为时间变量,其形式为 $C_0 + C_1 T + C_2 T^2 + \dots$。而本文的实现则统一使用儒略天数(Julian Days, $d$)作为变量。由于 1 儒略世纪 = 36525 天,笔者通过将原始公式中的 n 阶项系数 $C_n$ 除以 $36525^n$,将其转化为了适用于天数 $d$ 的等价形式。后续的时角等计算也做了类似的等价转换。
这种转换不影响计算的精度,但使得代码逻辑与以“天”为单位的 GLib.Date 时间体系更为统一。
我们将按照 Meeus 算法的流程,将天文学概念逐一转化为 Vala 代码。
时间基准:儒略日与 J2000.0 历元
天文学计算需要一个连续、无歧义的时间标尺。儒略日 (Julian Date, JD) 就是为此而生。我们通过 GLib 的 GLib.Date 可以轻松获取:
var date = new GLib.Date ();
date.set_dmy (day, month, year);
var julian_date = (double) date.get_julian ();
为了简化公式,天文学家选择了一个标准参考时刻,即 J2000.0 历元,对应于 2000 年 1 月 1 日国际原子时 12:00。我们的计算将以从这个历元开始的天数 $d$ 为基础。
这里减去 730120.5 即可将当天 00:00 UTC 转换为从 J2000.0 历元起算的天数。
// 从 J2000.0 历元起算的天数
double base_days_from_epoch = julian_date - 730120.5;
黄赤交角 (Obliquity of the Ecliptic, $\epsilon$)
地球自转轴相对于其公转轨道(黄道)的倾角。它随时间微小变化,Meeus 给出了一个拟合的多项式:
\[\epsilon (\text{deg}) = 23.439291111 - 0.0000003560347 d - 1.2285 \times 10^{-16} d^2 + 1.0335 \times 10^{-20} d^3\]其中 d 是从 J2000.0 起算的天数。在 Vala 中实现为:
double base_days_sq = base_days_from_epoch * base_days_from_epoch;
double base_days_cb = base_days_sq * base_days_from_epoch;
double obliquity_deg = 23.439291111 - 3.560347e-7 * base_days_from_epoch - 1.2285e-16 * base_days_sq + 1.0335e-20 * base_days_cb;
double obliquity_sin = Math.sin (obliquity_deg * DEG2RAD);
double obliquity_cos = Math.cos (obliquity_deg * DEG2RAD);
轨道参数
平黄经 (Mean Longitude, $L$) 和 平近点角 (Mean Anomaly, $M$) 是两个重要的轨道参数。在深入公式之前,有必要先理解这两个核心概念的物理意义。
平黄经 (Mean Longitude, $L$) 是想象一个“平均太阳”——它在一个完美的圆形轨道上,以恒定的速度运动,其周期与地球绕太阳的真实周期相同。平黄经就是这个“平均太阳”在黄道(地球公转轨道平面)上的角度位置。它的起点是春分点,因此平黄经为 0° 意味着“平均太阳”正处于春分点。
平近点角 (Mean Anomaly, $M$) 则描述了这个“平均太阳”在其理想化圆形轨道上,从“近地点”(轨道上离地球最近的点)出发所转过的角度。它是一个从 0° 到 360° 均匀增加的角度,反映了时间的流逝。当 $M$ 为 0° 时,意味着“平均太阳”在近地点;当 $M$ 为 180° 时,它在远地点。
简而言之,$L$ 告诉我们“平均太阳”在天空背景(黄道)上的位置,而 $M$ 则告诉我们它在其自身轨道路径上的进展。这两个“平”的、理想化的角度,是计算真实太阳位置(“真黄经”和“真近点角”)的起点。真实的太阳因为轨道是椭圆的(开普勒第一定律)且速度是变化的(开普勒第二定律),其位置会围绕着这个“平均太阳”前后摆动。
这些值描述了在一个理想化的匀速圆周轨道上太阳的位置。
\[L (\text{deg}) = 280.46645 + 0.98564736 d + 2.2727 \times 10^{-13} d^2\] \[M (\text{deg}) = 357.52772 + 0.985600282 d - 1.2016 \times 10^{-13} d^2 - 6.835 \times 10^{-20} d^3\]Vala 实现(注意 fmod 用于将角度归一化到 0-360 度):
double days_from_epoch_sq = days_from_epoch * days_from_epoch;
double days_from_epoch_cb = days_from_epoch_sq * days_from_epoch;
double mean_anomaly_deg = 357.52772 + 0.985600282 * days_from_epoch - 1.2016e-13 * days_from_epoch_sq - 6.835e-20 * days_from_epoch_cb;
mean_anomaly_deg = Math.fmod (mean_anomaly_deg, 360.0);
if (mean_anomaly_deg < 0) { mean_anomaly_deg += 360.0; }
double mean_longitude_deg = 280.46645 + 0.98564736 * days_from_epoch + 2.2727e-13 * days_from_epoch_sq;
mean_longitude_deg = Math.fmod (mean_longitude_deg, 360.0);
if (mean_longitude_deg < 0) { mean_longitude_deg += 360.0; }
中心差与真黄经 (Equation of Center and True Longitude, $\lambda$)
为了从“平”位置得到“真”位置,需要加上由地球轨道椭圆形引起的修正,即中心差。Meeus 算法给出了一个包含三项正弦修正的简化形式:
\[C (\text{deg}) = (1.914602 - 0.00000013188 d - 1.049 \times 10^{-14} d^2) \sin(M) + (0.019993 - 0.0000000027652 d) \sin(2M) + 0.000289 \sin(3M)\]真黄经 (True Longitude, $\lambda$) 就是平黄经加上中心差:
\[\lambda = L + C\]Vala 实现:
double ecliptic_c1 = 1.914602 - 1.3188e-7 * base_days_from_epoch - 1.049e-14 * base_days_sq;
double ecliptic_c2 = 0.019993 - 2.7652e-9 * base_days_from_epoch;
const double ecliptic_c3 = 0.000289;
double mean_anomaly_rad = mean_anomaly_deg * DEG2RAD;
double equation_of_center_deg = ecliptic_c1 * Math.sin (mean_anomaly_rad)
+ ecliptic_c2 * Math.sin (2.0 * mean_anomaly_rad)
+ ecliptic_c3 * Math.sin (3.0 * mean_anomaly_rad);
double ecliptic_longitude_deg = mean_longitude_deg + equation_of_center_deg;
坐标转换:从黄道到赤道
有了真黄经 λ 和黄赤交角 ε,我们便可将太阳位置转换到赤道坐标系,得到赤纬 (Declination, δ) 和赤经 (Right Ascension, RA)。
Vala 实现:
double ecliptic_longitude_rad = ecliptic_longitude_deg * DEG2RAD;
double ecliptic_longitude_sin = Math.sin (ecliptic_longitude_rad);
double ecliptic_longitude_cos = Math.cos (ecliptic_longitude_rad);
// 计算赤纬
double declination_sin = (obliquity_sin * ecliptic_longitude_sin).clamp (-1.0, 1.0);
double declination_rad = Math.asin (declination_sin);
// 计算赤经
double right_ascension_rad = Math.atan2 (obliquity_cos * ecliptic_longitude_sin, ecliptic_longitude_cos);
应用一:计算太阳高度角
有了太阳的赤纬 δ,我们距离计算出它的高度角只有一步之遥。最后一步是计算出在给定的地方、给定的时刻,太阳相对于观测者的方位,这由时角 (Hour Angle, $HA$) 来描述。
真太阳时 (True Solar Time, $TST$)
我们日常使用的钟表时间是地方标准时 (Local Standard Time),它基于一个时区(如 UTC+8)的中央经线,并非我们所在地的真实太阳位置。要计算时角,我们必须首先将钟表时间转换为真太阳时 (TST),即由日晷测得的时间。
转换过程考虑了两个主要修正:
-
均时差 (Equation of Time, EoT):因地球轨道偏心率和黄赤交角引起的修正。我们的钟表以恒定速度走时,但真实太阳的视运动并不均匀。由于地球轨道是椭圆的,太阳在近日点附近运动较快,在远日点附近运动较慢;同时,黄赤交角使得太阳在黄道上的运动投影到天赤道时速度不均。这两个主要效应叠加,使真实太阳过中天的时刻相对于“平均太阳”可相差最多约 ±16 分钟。
均时差本质上是平太阳时角与真太阳时角之差,可通过比较“平均太阳”的赤经(由平黄经 $L$ 计算:$T_\text{mean} = L/15$)与真太阳的赤经(前面已求得的
right_ascension_rad)来获得: $EoT_\text{minutes} = (T_\text{mean,hours} - RA_\text{hours}) \times 60$ -
经度修正:我们的钟表时间基于时区中央经线,但太阳过中天(正午)的时刻取决于我们真实的经度。经度每向东 1°,正午就提早 4 分钟。
因此,真太阳时的计算公式为:
\[TST_\text{minutes} = T_\text{local, minutes} + EoT_\text{minutes} + 4 \times \lambda_\text{lon, deg} - 60 \times TZ_\text{offset, hr}\]其中:
- $T_\text{local, minutes}$ 是午夜起算的本地钟表时间(分钟)。
- $EoT_\text{minutes}$ 是我们计算出的均时差(分钟)。
- $\lambda_\text{lon, deg}$ 是观测地的地理经度(东经为正)。
- $TZ_\text{offset, hr}$ 是时区偏移量(例如 UTC+8 时区为 8)。
在我们的 Vala 代码中,tst_offset 预先计算了经度和时区带来的固定偏移,而 eqtime_minutes 则是动态计算的均时差。
// 均时差 (分钟)
double eot_hours = mean_time - right_ascension_hours;
double eqtime_minutes = eot_hours * 60.0;
// 固定的经度与时区偏移 (分钟)
double tst_offset = 4.0 * longitude_deg - 60.0 * timezone_offset_hrs;
// i 是午夜起算的本地时间(分钟)
double tst_minutes = i + eqtime_minutes + tst_offset;
时角 (Hour Angle, $HA$)
时角定义为天体距离本地子午线(正南或正北的天空弧线)的角度。天文学上通常定义正午时为 0°,下午为正,上午为负。地球每小时自转 15°,每 4 分钟自转 1°。
从以分钟计量的真太阳时到以度计量的时角,转换公式为:
\[HA_\text{deg} = \frac{TST_\text{minutes}}{4} - 180\]这里除以 4 是因为 1 分钟时间对应 0.25° 的旋转。减去 180° 是为了将计时起点从午夜(0 分钟)校正到正午(720 分钟),使得正午时 $720 / 4 - 180 = 0$。
// 将真太阳时转换为时角 (度)
double hour_angle_deg = tst_minutes / 4.0 - 180.0;
double hour_angle_rad = hour_angle_deg * DEG2RAD;
太阳高度角 (Altitude, $\alpha$)
最后,我们将观测地纬度 $\phi$、太阳赤纬 $\delta$ 和刚刚得到的时角 $\mathrm{HA}$ 代入球面三角学的基本公式,即可求得太阳高度角 $\alpha$。
\[\sin(\alpha) = \sin(\phi)\sin(\delta) + \cos(\phi)\cos(\delta)\cos(HA)\]在高精度下,我们还需要考虑地心视差 (Geocentric Parallax)。上述公式计算的是地心坐标系下的太阳高度角,而观测者位于地球表面。由于地球半径相对于日地距离不可忽略,观测者看到的太阳位置会比地心看到的略低。修正公式为:
\[\Delta \alpha = - \arcsin \left( \frac{R_\oplus}{R} \cos \alpha \right) \approx -0.00244^\circ \times \cos \alpha\]虽然这个修正量很小(最大约 8.8 角秒,即 0.00244°),但在高精度计算中却可能成为系统误差的主要来源。
 |
|---|
| 视差修正前的 Meeus 算法误差分布直方图 |
 |
| 视差修正后的 Meeus 算法误差分布直方图 |
在加入地心视差修正前,可以在图上明显看到分布峰值在 0.0020° 而不是 0°;加入修正后,误差分布则基本关于 0° 对称,显著提升了计算的准确性。
// 计算太阳高度角的正弦值
double elevation_sin = (sin_lat * declination_sin + cos_lat * declination_cos * Math.cos (hour_angle_rad)).clamp (-1.0, 1.0);
double elevation_cos = Math.sqrt (1.0 - elevation_sin * elevation_sin);
// 地心视差修正 (度)
double geocentric_parallax_deg = 0.00244 * elevation_cos;
// 反正弦后转换为度,并减去视差
sun_angles[i] = Math.asin (elevation_sin) * RAD2DEG - geocentric_parallax_deg;
至此,我们就完成了从一个日期和时间点,到其精确太阳高度角的完整计算链条。
大气折射修正 (Atmospheric Refraction Correction)
除了视差,大气折射也是影响地基观测的重要因素。当光线穿过地球大气层时,由于大气密度的变化,光线会发生弯曲,使得天体的视位置比真位置要高。
本程序使用了 Saemundsson 公式 来估算大气折射量 $R$(单位:度):
\[R = 1.02 \cot \left( h + \frac{10.3}{h + 5.11} \right) \times \frac{1}{60}\]其中 $h$ 是真高度角(单位:度)。值得注意的是,该公式在数学上存在适用范围。当真高度角 $h$ 过低(小于约 -5.0015°)或接近天顶(大于约 89.8915°)时,公式计算出的修正值会变为负数,不合理。因此,我们在代码中加入了范围检查,仅在 $-5.0015^\circ < h < 89.8915^\circ$ 的范围内应用此修正,超出范围则视为无折射。
考虑到大气折射受温度、气压等气象条件影响较大,我们在界面上提供了一个 Refraction 调节项(refraction_factor),允许用户调整折射修正的强度。设置为 1.0 表示标准大气条件下的修正,设置为 0.0 则关闭修正。
需要注意的是,本文后续的精度验证是在无大气折射的理想情况下进行的,验证的是真实的几何角度而非目测角度。开启大气折射修正后,计算结果将更接近实际观测值,但具体偏差将取决于实际的大气环境。
地日距离 (Earth-Sun Distance)
除了太阳的方位,我们还可以计算地球到太阳的距离。这首先需要地球轨道的离心率 (Eccentricity, $e$),它也随时间微小变化:
\[e = 0.016708634 - 1.15091 \times 10^{-9} d - 9.497 \times 10^{-17} d^2\]接下来,我们需要真近点角 (True Anomaly, $\nu$),即行星在其轨道上相对于近心点(离中心天体最近的点)的角度。它等于平近点角 $M$ 加上中心差 $C$:
\[\nu = M + C\]有了离心率和真近点角,就可以根据活力公式的变体,计算出以天文单位(AU)为单位的日地距离 $R$:
\[R_\text{AU} = \frac{a(1 - e^2)}{1 + e \cos(\nu)}\]其中 $a$ 是半长轴,对于日地距离,我们近似为 1 AU。最后,我们将它转换为公里(km)。
Vala 实现:
double eccentricity = 0.016708634 - 1.15091e-09 * base_days_from_epoch - 9.497e-17 * base_days_sq;
double true_anomaly_rad = mean_anomaly_rad + equation_of_center_deg * DEG2RAD;
double distance_au = (1.0 - eccentricity * eccentricity) / (1.0 + eccentricity * Math.cos (true_anomaly_rad));
// sun_distances[i] = distance_au * 149597870.7; // 转换为 km
应用二:计算日出日落时间及白昼时长
计算日出日落时间与白昼时长是这些天文参数的另一个直接应用。其核心是计算出太阳升起和落下的时刻,即太阳高度角为某个特定值(通常是-0.83°而不是0,考虑大气折射)时的时角。
一个常见的近似是假设太阳赤纬和均时差在一天之内是恒定的,取正午时刻的值,然后直接解算日出/日落时角。然而,太阳的赤纬和均时差在一天中是持续变化的,尤其是在高纬度地区或对精度要求高的场景下,这种简化会引入不可忽略的误差,与笔者使用的 Meeus 算法精度不匹配,因此笔者并没有这样使用。
需要注意的是,在计算日出日落时,我们通常不单独计算地心视差。这是因为日出日落的标准定义通常已经包含了一个综合的修正角(如 -0.833°),它涵盖了太阳半径(约 0.266°)、大气折射(约 0.566°)以及微小的视差修正。此外,大气折射受温度、气压影响极大,其不确定性远大于视差修正,因此在允许用户调节地平线修正角(Horizon Angle)的算法中,将视差视为常数合并处理是合理的做法。
为了获得更高的精度,笔者采用了一种迭代逼近的方法。其基本思想是:先用一个初始值(如正午的太阳参数)估算出大致的日出日落时间,然后用这个估算出的时间点重新计算更精确的太阳参数,再用新参数反过来修正日出日落时间,如此往复,直到结果收敛。
获取正午时刻的太阳参数作为初始值
与应用一类似,我们首先计算出当天正午(12:00)时刻的太阳赤纬 $\delta$ 和均时差 $EoT$。这为我们的迭代提供了一个合理的起点。
求解初始的日出/日落时角 ($\omega_0$)
将太阳高度角公式反解,求解时角 $\mathrm{HA}$。设 $\alpha$ 为大气折射导致的观测地平线修正角(一般取 $-0.83^\circ$),$\phi$ 为本地纬度,$\delta$ 为太阳赤纬,则日落时的时角 $\omega_0$ 满足:
\[\cos(\omega_0) = \frac{\sin(\alpha) - \sin(\phi)\sin(\delta)}{\cos(\phi)\cos(\delta)}\]此时需要处理边界情况:
- 若 $\cos(\omega_0) \geq 1$,意味着太阳永远在地平线以下,发生极夜。
- 若 $\cos(\omega_0) \leq -1$,意味着太阳永远在地平线以上,发生极昼。
计算初始的日出日落时间
太阳时角 $\omega_0$ 代表了从正午到日落的时间跨度(以角度计)。本地钟表的日出/日落时间还需考虑均时差和经度/时区修正。
\[T_\text{sunrise} = 12 - \frac{\omega_0}{15^\circ/\text{hr}} - \frac{EoT_\text{minutes} + \text{LonCorr}_\text{minutes}}{60}\] \[T_\text{sunset} = 12 + \frac{\omega_0}{15^\circ/\text{hr}} - \frac{EoT_\text{minutes} + \text{LonCorr}_\text{minutes}}{60}\]迭代优化
- 日出时间优化:将上一步得到的 $T_\text{sunrise}$ 作为新的时间点,重新计算该时刻精确的太阳赤纬 $\delta_\text{sunrise}$ 和均时差 $EoT_\text{sunrise}$。将新参数代入步骤 2 和 3,得到一个更精确的日出时间 $T’_\text{sunrise}$。
- 日落时间优化:同理,用 $T_\text{sunset}$ 计算出 $\delta_\text{sunset}$ 和 $EoT_\text{sunset}$,得到更精确的日落时间 $T’_\text{sunset}$。
- 重复此过程,直到连续两次计算出的日出、日落时间变化足够小,迭代收敛。实际上一般只需要1次迭代即可达到0.1秒以内的精度。
计算总昼长
最终的白昼时长即为精确的日落时间减去日出时间:
\[t_\text{daylight} = T_\text{sunset, final} - T_\text{sunrise, final}\]通过这种迭代方法,我们充分考虑了太阳参数在一天内的动态变化,从而获得了更精确的日出日落时间和白昼时长,避免了简化假设带来的误差。
Vala 在数值计算中的优势
通过这个实践,我们可以总结出 Vala 在处理此类问题时的几个优点:
- 卓越性能:Vala 直接编译为C代码,几乎没有额外开销。对于包含大量循环和浮点运算的数值计算任务,其性能表现与手写C代码相当,远超各类解释型语言。
- 代码可读性与组织性:相比C,Vala 提供了类、方法、属性等现代面向对象特性,使得我们可以将复杂的计算逻辑封装在独立的、职责清晰的函数或类中,代码结构更优,可维护性更强。
- 类型安全:Vala 强类型系统能在编译期捕获大量潜在错误,这对于处理多步骤、易出错的复杂科学计算流程至关重要。
- 底层库的便捷访问:能够零成本地调用 GLib/GObject 库是 Vala 的一大杀手锏。如本文中直接使用
GLib.Date.get_julian(),极大地简化了时间处理的复杂度。
总结
本文通过一个完整的天文算法实践,展示了 Vala 作为一门通用语言,在图形界面开发之外,同样是执行高性能数值计算的有力工具。它在提供接近C的性能的同时,赋予了我们更现代化、更安全的编程范式。
希望这次从理论到代码的深度实践,能为你提供一个在 Vala 中进行科学计算的优秀范例,并激发你使用 Vala 探索更多可能性的兴趣。
效果及计算代码
效果
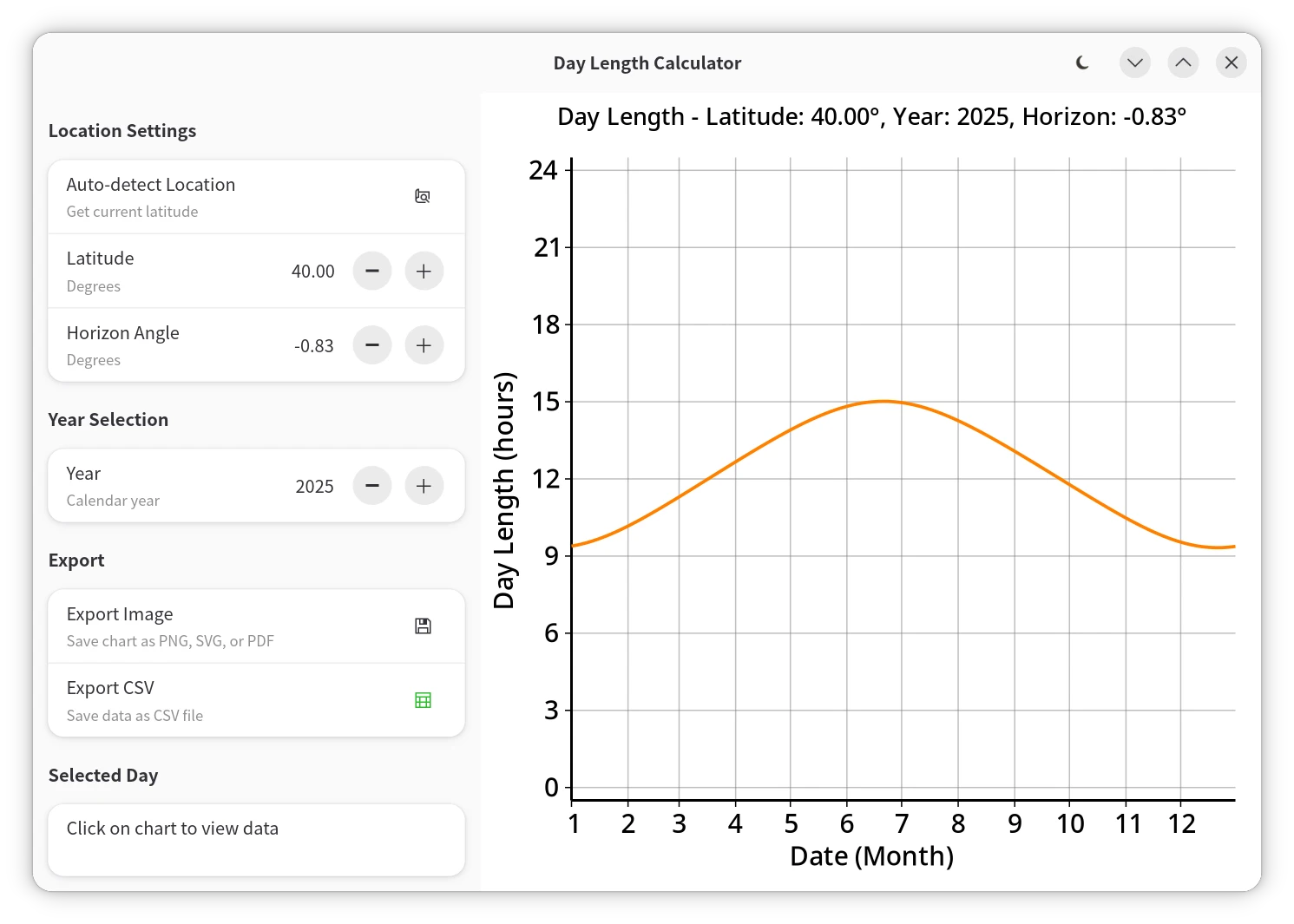
笔者将上述算法应用于 GUI 程序中,结合 GTK4/Libadwaita/JSON-GLib等技术栈,制作了一个太阳高度角计算器和一个白昼时长计算器,将计算结果可视化展示。两个程序均支持浅色和深色主题,并能自动从 IP 获取地理位置,自动识别时区,还支持导出 PNG、SVG、PDF 等格式的图表,以及 CSV 数据。
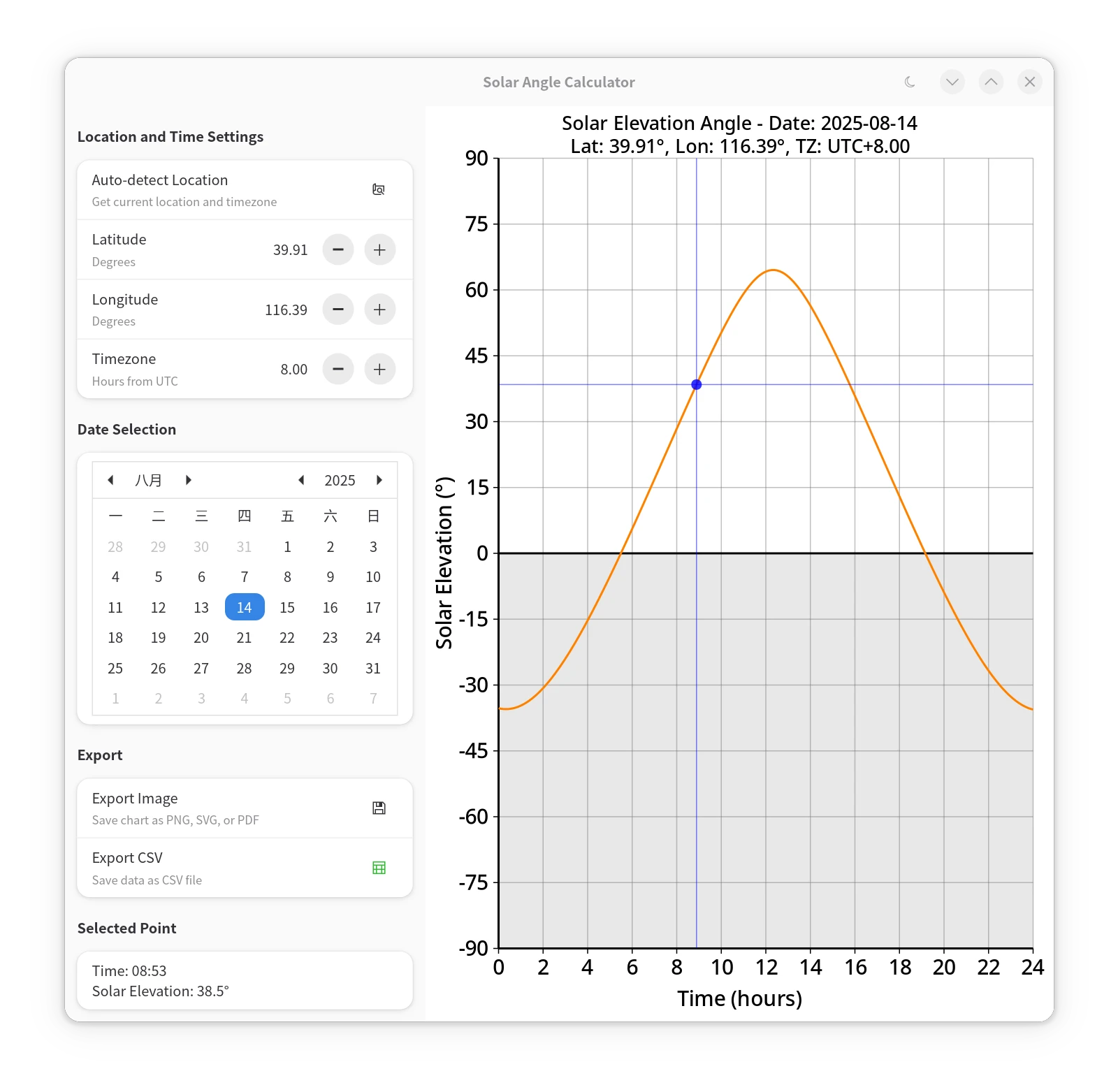 |
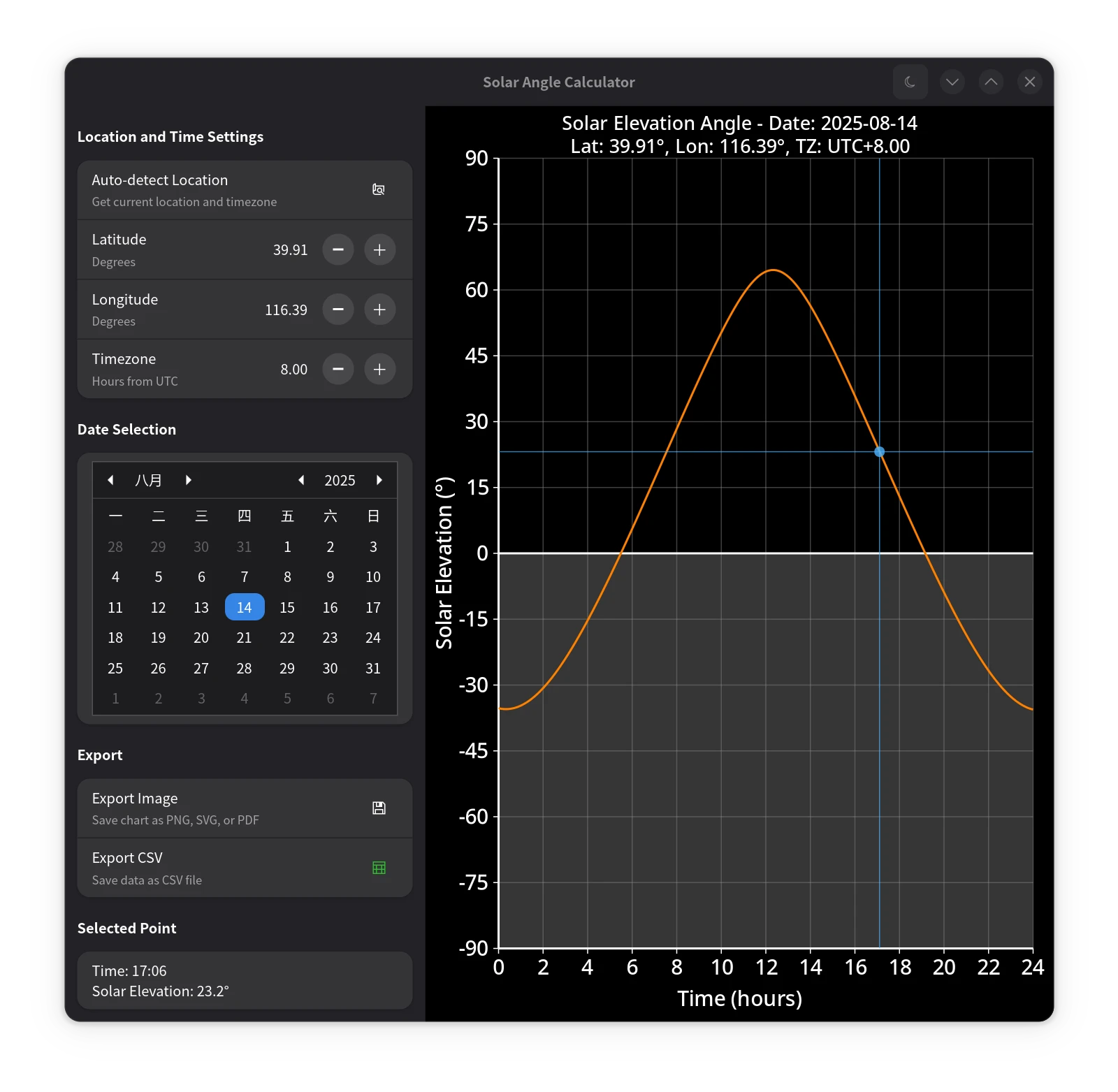 |
|---|---|
| 太阳高度角计算器(浅色模式) | 太阳高度角计算器(深色模式) |
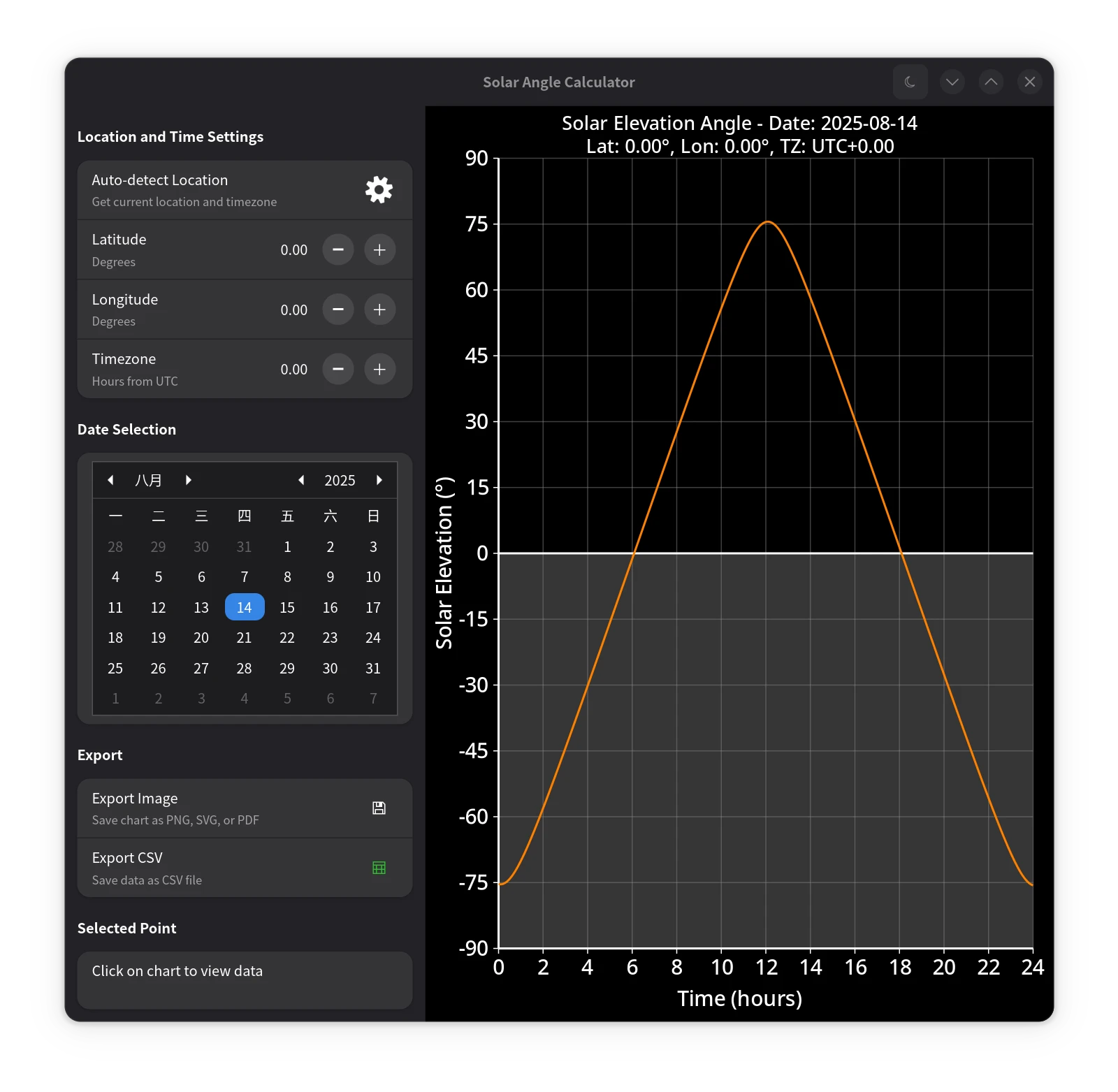 |
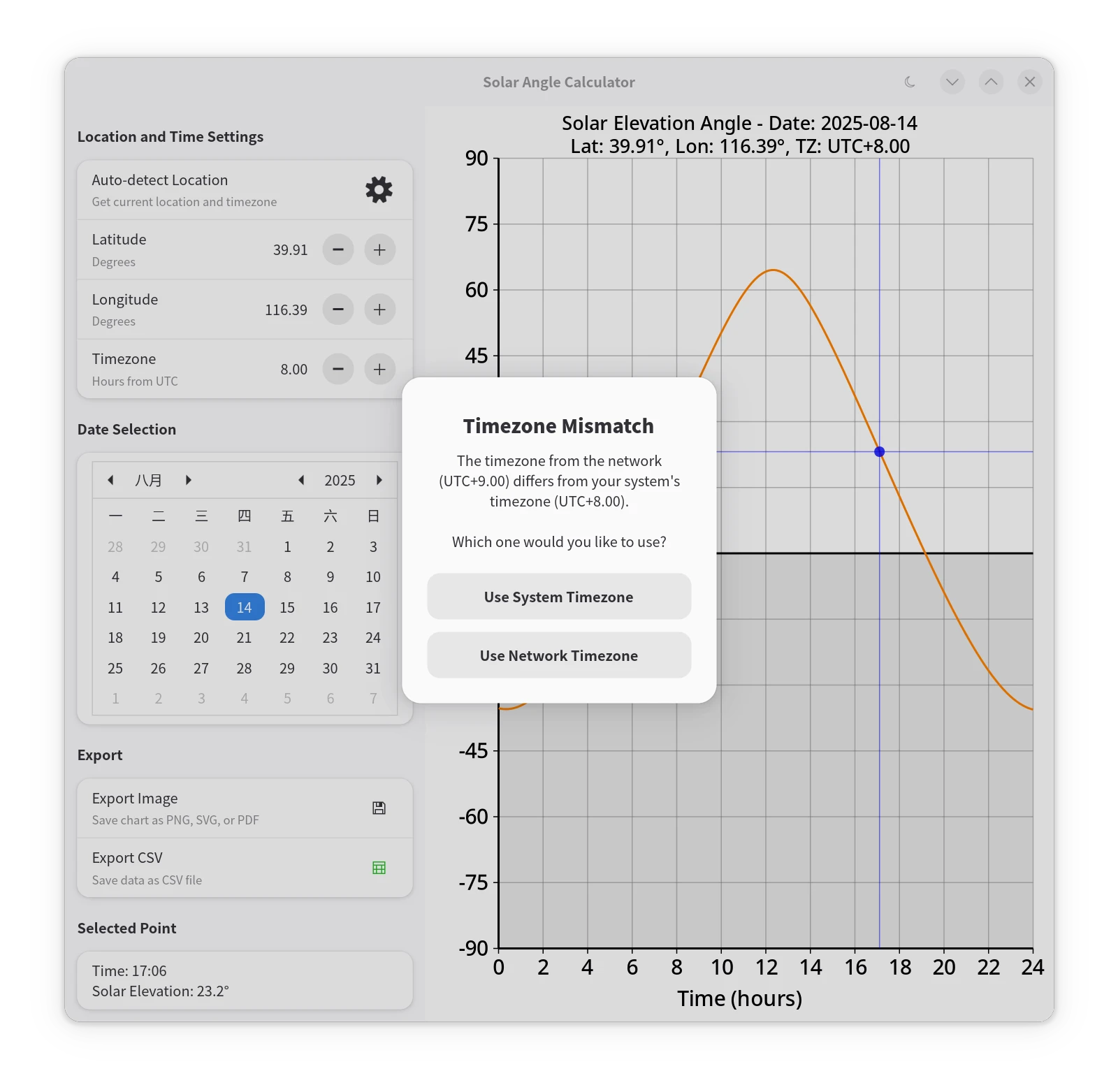 |
| 获取地理位置时的加载动画 | 提示与选择 |
 |
 |
|---|---|
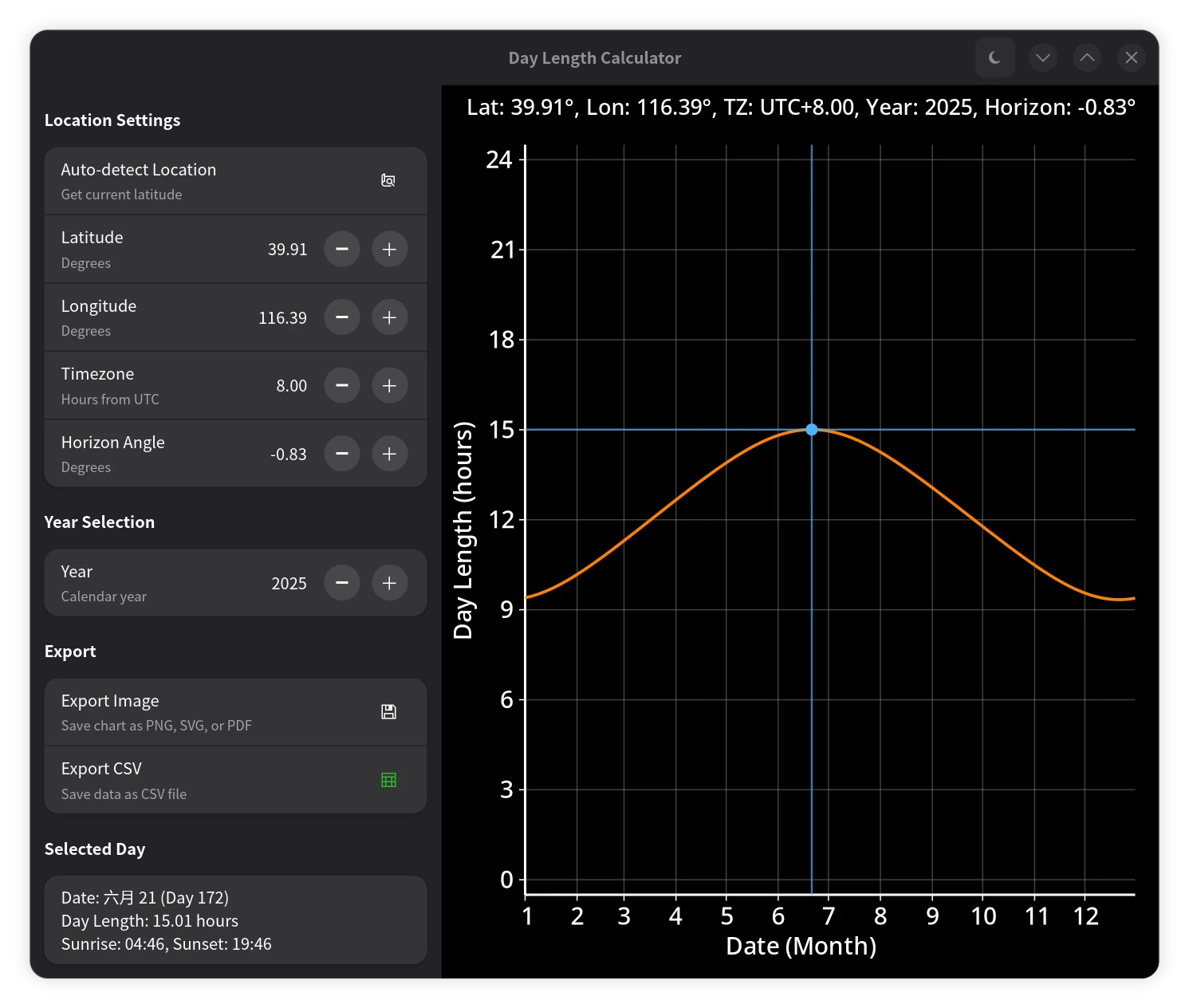
| 白昼时长计算器(浅色模式) | 白昼时长计算器(深色模式) |
太阳高度角计算
该函数可以用于计算一天中每分钟的太阳高度角,完整程序见 GitHub:
/**
* Calculates solar elevation angles for each minute of the day.
* Based on Meeus's book "Astronomical Algorithms" (1998)
*
* @param latitude_rad Latitude in radians.
* @param longitude_deg Longitude in degrees.
* @param timezone_offset_hrs Timezone offset from UTC in hours.
* @param julian_date GLib's Julian Date for the day (from 0001-01-01).
*/
private void generate_sun_angles (double latitude_rad, double longitude_deg, double timezone_offset_hrs, double julian_date) {
double sin_lat = Math.sin (latitude_rad);
double cos_lat = Math.cos (latitude_rad);
// Base days from J2000.0 epoch (GLib's Julian Date is days since 0001-01-01 12:00 UTC)
double base_days_from_epoch = julian_date - 730120.5; // julian_date's 00:00 UTC to 2000-01-01 12:00 UTC
// Pre-compute obliquity with higher-order terms (changes very slowly)
double base_days_sq = base_days_from_epoch * base_days_from_epoch;
double base_days_cb = base_days_sq * base_days_from_epoch;
double obliquity_deg = 23.439291111 - 3.560347e-7 * base_days_from_epoch - 1.2285e-16 * base_days_sq + 1.0335e-20 * base_days_cb;
double obliquity_sin = Math.sin (obliquity_deg * DEG2RAD);
double obliquity_cos = Math.cos (obliquity_deg * DEG2RAD);
double ecliptic_c1 = 1.914602 - 1.3188e-7 * base_days_from_epoch - 1.049e-14 * base_days_sq;
double ecliptic_c2 = 0.019993 - 2.7652e-9 * base_days_from_epoch;
double tst_offset = 4.0 * longitude_deg - 60.0 * timezone_offset_hrs;
double eccentricity = 0.016708634 - 1.15091e-09 * base_days_from_epoch - 9.497e-17 * base_days_sq;
for (int i = 0; i < RESOLUTION_PER_MIN; i += 1) {
double days_from_epoch = base_days_from_epoch + (i / 60.0 - timezone_offset_hrs) / 24.0;
double days_from_epoch_sq = days_from_epoch * days_from_epoch;
double days_from_epoch_cb = days_from_epoch_sq * days_from_epoch;
double mean_anomaly_deg = 357.52772 + 0.985600282 * days_from_epoch - 1.2016e-13 * days_from_epoch_sq - 6.835e-20 * days_from_epoch_cb;
mean_anomaly_deg = Math.fmod (mean_anomaly_deg, 360.0);
if (mean_anomaly_deg < 0) {
mean_anomaly_deg += 360.0;
}
double mean_longitude_deg = 280.46645 + 0.98564736 * days_from_epoch + 2.2727e-13 * days_from_epoch_sq;
mean_longitude_deg = Math.fmod (mean_longitude_deg, 360.0);
if (mean_longitude_deg < 0) {
mean_longitude_deg += 360.0;
}
double mean_anomaly_rad = mean_anomaly_deg * DEG2RAD;
double equation_of_center_deg = ecliptic_c1 * Math.sin (mean_anomaly_rad)
+ ecliptic_c2 * Math.sin (2.0 * mean_anomaly_rad)
+ 0.000289 * Math.sin (3.0 * mean_anomaly_rad);
double ecliptic_longitude_deg = mean_longitude_deg + equation_of_center_deg;
ecliptic_longitude_deg = Math.fmod (ecliptic_longitude_deg, 360.0);
if (ecliptic_longitude_deg < 0) {
ecliptic_longitude_deg += 360.0;
}
double ecliptic_longitude_rad = ecliptic_longitude_deg * DEG2RAD;
double ecliptic_longitude_sin = Math.sin (ecliptic_longitude_rad);
double ecliptic_longitude_cos = Math.cos (ecliptic_longitude_rad);
double declination_sin = (obliquity_sin * ecliptic_longitude_sin).clamp (-1.0, 1.0);
double declination_cos = Math.sqrt (1.0 - declination_sin * declination_sin);
double mean_time_hours = mean_longitude_deg / 15.0;
double right_ascension_hours = Math.atan2 (obliquity_cos * ecliptic_longitude_sin, ecliptic_longitude_cos) * RAD2DEG / 15.0;
if (right_ascension_hours < 0) {
right_ascension_hours += 24.0;
}
double delta_ra = right_ascension_hours - mean_time_hours;
if (delta_ra > 12.0) {
right_ascension_hours -= 24.0;
} else if (delta_ra < -12.0) {
right_ascension_hours += 24.0;
}
double eqtime_minutes = (mean_time_hours - right_ascension_hours) * 60.0;
double hour_angle_rad = ((i + eqtime_minutes + tst_offset) / 4.0 - 180.0) * DEG2RAD;
double elevation_sin = (sin_lat * declination_sin + cos_lat * declination_cos * Math.cos (hour_angle_rad)).clamp (-1.0, 1.0);
double elevation_cos = Math.sqrt (1.0 - elevation_sin * elevation_sin); // non-negative in [-90 deg, +90 deg]
double geocentric_parallax_deg = 0.00244 * elevation_cos;
double true_elevation_deg = Math.asin (elevation_sin) * RAD2DEG - geocentric_parallax_deg;
sun_angles[i] = true_elevation_deg + calculate_refraction (true_elevation_deg, refraction_factor);
double true_anomaly_rad = mean_anomaly_rad + equation_of_center_deg * DEG2RAD;
double distance_au = (1.0 - eccentricity * eccentricity) / (1.0 + eccentricity * Math.cos (true_anomaly_rad));
sun_distances[i] = distance_au * 149597870.7; // Convert AU to km
}
}
/**
* Updates solar angle data for current settings.
*/
private void update_plot_data () {
double latitude_rad = latitude * DEG2RAD;
// Convert DateTime to Date and get Julian Day Number
var date = Date ();
date.set_dmy ((DateDay) selected_date.get_day_of_month (),
selected_date.get_month (),
(DateYear) selected_date.get_year ());
var julian_date = (double) date.get_julian ();
generate_sun_angles (latitude_rad, longitude, timezone_offset_hours, julian_date);
// Clear click point when data updates
has_click_point = false;
click_info_label.label = DEFAULT_INFO_LABEL;
}
/**
* Calculates atmospheric refraction using Saemundsson's formula.
*
* The formula R = 1.02 / tan(h + 10.3/(h+5.11)) mathematically fails
* when the inner argument exceeds 90 degrees or creates a singularity.
* The roots are exactly ~ -5.0015 and ~ 89.8915.
* Inside this range, the formula is valid.
*
* @param true_elevation_deg True elevation angle in degrees.
* @param refraction_factor Factor to scale the refraction effect.
*/
private static double calculate_refraction (double true_elevation_deg, double refraction_factor) {
if (refraction_factor == 0.0) {
return 0.0;
}
if (true_elevation_deg > 89.8915 || true_elevation_deg < -5.0015) {
return 0.0;
}
double angle_arg = (true_elevation_deg + 10.3 / (true_elevation_deg + 5.11)) * DEG2RAD;
return 1.02 / 60.0 / Math.tan (angle_arg) * refraction_factor;
}
日出日落时间及白昼时长计算
该函数用于计算某地某一天的日出日落时间及白昼时长,完整程序见 GitHub:
/**
* Compute solar parameters at a given local time.
*
* @param base_days_from_epoch Days from J2000.0 epoch at UTC midnight
* @param time_local_hours Local time in hours [0,24)
* @param obliquity_sin Sine of obliquity
* @param obliquity_cos Cosine of obliquity
* @param ecliptic_c1 Ecliptic longitude correction coefficient 1
* @param ecliptic_c2 Ecliptic longitude correction coefficient 2
*/
private static inline void compute_solar_parameters (
double base_days_from_epoch, double time_local_hours,
double obliquity_sin, double obliquity_cos,
double ecliptic_c1, double ecliptic_c2,
out double out_declination_sin, out double out_declination_cos, out double out_eqtime_minutes
) {
double days_from_epoch = base_days_from_epoch + time_local_hours / 24.0;
double days_sq = days_from_epoch * days_from_epoch;
double days_cb = days_sq * days_from_epoch;
// Mean anomaly
double mean_anomaly_deg = 357.52772 + 0.985600282 * days_from_epoch - 1.2016e-13 * days_sq - 6.835e-20 * days_cb;
double mean_anomaly_rad = mean_anomaly_deg * DEG2RAD;
// Mean longitude (normalized)
double mean_longitude_deg = Math.fmod (280.46645 + 0.98564736 * days_from_epoch + 2.2727e-13 * days_sq, 360.0);
if (mean_longitude_deg < 0) {
mean_longitude_deg += 360.0;
}
// Ecliptic longitude
double ecliptic_longitude_deg = mean_longitude_deg
+ ecliptic_c1 * Math.sin (mean_anomaly_rad)
+ ecliptic_c2 * Math.sin (2.0 * mean_anomaly_rad)
+ 0.000289 * Math.sin (3.0 * mean_anomaly_rad);
double ecliptic_longitude_rad = ecliptic_longitude_deg * DEG2RAD;
double ecliptic_longitude_sin = Math.sin (ecliptic_longitude_rad);
double ecliptic_longitude_cos = Math.cos (ecliptic_longitude_rad);
// Declination
out_declination_sin = (obliquity_sin * ecliptic_longitude_sin).clamp (-1.0, 1.0);
out_declination_cos = Math.sqrt (1.0 - out_declination_sin * out_declination_sin);
// Equation of time
double right_ascension_rad = Math.atan2 (obliquity_cos * ecliptic_longitude_sin, ecliptic_longitude_cos);
double right_ascension_hours = right_ascension_rad * RAD2DEG / 15.0;
double mean_time_hours = mean_longitude_deg / 15.0;
double time_diff = mean_time_hours - right_ascension_hours;
if (time_diff > 12.0) {
time_diff -= 24.0;
} else if (time_diff < -12.0) {
time_diff += 24.0;
}
out_eqtime_minutes = time_diff * 60.0;
}
/**
* Calculates day length, sunrise, and sunset times.
* Based on Meeus's book "Astronomical Algorithms" (1998)
*
* @param latitude_rad Latitude in radians.
* @param longitude_deg Longitude in degrees.
* @param timezone_offset_hrs Timezone offset in hours from UTC.
* @param julian_date GLib's Julian Date for the day (from 0001-01-01).
* @param horizon_angle_deg Horizon angle correction in degrees (default -0.83° for atmospheric refraction).
* @param day_length Output parameter for day length in hours.
* @param sunrise_time Output parameter for sunrise time in local hours [0,24).
* @param sunset_time Output parameter for sunset time in local hours [0,24).
*/
private void calculate_day_length (
double latitude_rad, double longitude_deg, double timezone_offset_hrs, double julian_date, double horizon_angle_deg,
out double day_length, out double sunrise_time, out double sunset_time
) {
double sin_lat = Math.sin (latitude_rad);
double cos_lat = Math.cos (latitude_rad);
double sin_horizon = Math.sin (horizon_angle_deg * DEG2RAD);
double base_days_from_epoch_utc_midnight = (julian_date - 730120.5) - timezone_offset_hrs / 24.0;
// Obliquity
double base_days_sq = base_days_from_epoch_utc_midnight * base_days_from_epoch_utc_midnight;
double base_days_cb = base_days_sq * base_days_from_epoch_utc_midnight;
double obliquity_deg = 23.439291111 - 3.560347e-7 * base_days_from_epoch_utc_midnight - 1.2285e-16 * base_days_sq + 1.0335e-20 * base_days_cb;
double obliquity_sin = Math.sin (obliquity_deg * DEG2RAD);
double obliquity_cos = Math.cos (obliquity_deg * DEG2RAD);
// Ecliptic correction coefficients
double ecliptic_c1 = 1.914602 - 1.3188e-7 * base_days_from_epoch_utc_midnight - 1.049e-14 * base_days_sq;
double ecliptic_c2 = 0.019993 - 2.7652e-9 * base_days_from_epoch_utc_midnight;
double tst_offset = 4.0 * longitude_deg - 60.0 * timezone_offset_hrs;
// Initial estimate at noon
double declination_sin, declination_cos, eqtime_minutes;
compute_solar_parameters (
base_days_from_epoch_utc_midnight, 12.0,
obliquity_sin, obliquity_cos, ecliptic_c1, ecliptic_c2,
out declination_sin, out declination_cos, out eqtime_minutes
);
double cos_ha = (sin_horizon - sin_lat * declination_sin) / (cos_lat * declination_cos);
if (cos_ha >= 1.0) {
day_length = 0.0;
sunrise_time = double.NAN;
sunset_time = double.NAN;
return;
} else if (cos_ha <= -1.0) {
day_length = 24.0;
sunrise_time = double.NAN;
sunset_time = double.NAN;
return;
}
double ha_deg = Math.acos (cos_ha) * RAD2DEG;
sunrise_time = 12.0 - ha_deg / 15.0 - (eqtime_minutes + tst_offset) / 60.0;
sunset_time = 12.0 + ha_deg / 15.0 - (eqtime_minutes + tst_offset) / 60.0;
// Iterative refinement
const double TOL_HOURS = 0.1 / 3600.0;
for (int iter = 0; iter < 5; iter += 1) {
double old_sr = sunrise_time;
double old_ss = sunset_time;
compute_solar_parameters (
base_days_from_epoch_utc_midnight, sunrise_time,
obliquity_sin, obliquity_cos, ecliptic_c1, ecliptic_c2,
out declination_sin, out declination_cos, out eqtime_minutes
);
cos_ha = (sin_horizon - sin_lat * declination_sin) / (cos_lat * declination_cos);
if (cos_ha >= 1.0 || cos_ha <= -1.0) {
break;
}
ha_deg = Math.acos (cos_ha) * RAD2DEG;
sunrise_time = 12.0 - ha_deg / 15.0 - (eqtime_minutes + tst_offset) / 60.0;
compute_solar_parameters (
base_days_from_epoch_utc_midnight, sunset_time,
obliquity_sin, obliquity_cos, ecliptic_c1, ecliptic_c2,
out declination_sin, out declination_cos, out eqtime_minutes
);
cos_ha = (sin_horizon - sin_lat * declination_sin) / (cos_lat * declination_cos);
if (cos_ha >= 1.0 || cos_ha <= -1.0) {
break;
}
ha_deg = Math.acos (cos_ha) * RAD2DEG;
sunset_time = 12.0 + ha_deg / 15.0 - (eqtime_minutes + tst_offset) / 60.0;
if (Math.fabs (sunrise_time - old_sr) < TOL_HOURS && Math.fabs (sunset_time - old_ss) < TOL_HOURS) {
break;
}
}
// Normalize to [0, 24)
sunrise_time = Math.fmod (sunrise_time, 24.0);
if (sunrise_time < 0) {
sunrise_time += 24.0;
}
sunset_time = Math.fmod (sunset_time, 24.0);
if (sunset_time < 0) {
sunset_time += 24.0;
}
day_length = sunset_time - sunrise_time;
if (day_length < 0) {
day_length += 24.0;
}
}
/**
* Updates plot data for all days in the selected year.
*/
private void update_plot_data () {
int total_days = (selected_year % 4 == 0 && (selected_year % 100 != 0 || selected_year % 400 == 0)) ? 366 : 365;
day_lengths = new double[total_days];
sunrise_times = new double[total_days];
sunset_times = new double[total_days];
double latitude_rad = latitude * DEG2RAD;
// Get Julian Date for January 1st of the selected year
var date = Date ();
date.set_dmy (1, 1, (DateYear) selected_year);
uint base_julian_date = date.get_julian ();
for (int day = 0; day < total_days; day += 1) {
calculate_day_length (
latitude_rad, longitude, timezone_offset_hours, (double) (base_julian_date + day), horizon_angle,
out day_lengths[day], out sunrise_times[day], out sunset_times[day]
);
}
// Clear click point when data updates
has_click_point = false;
click_info_label.label = "Click on chart to view data\n\n";
}
附录:算法精度对比验证
为了全面评估本文所采用的 Meeus 算法的精度,并将其与其他常见算法进行横向对比,笔者编写了一个 Python 验证脚本。该脚本将以下几种算法的计算结果与业界公认的高精度方法——astropy 库的计算结果进行逐小时比较:
- Meeus 算法 (无视差修正):即
generate_sun_angles_meeus,这是 Meeus 算法的标准实现,但未包含地心视差修正。我们将看到,这会引入一个微小的系统误差。 - MeeusFixed 算法 (含视差修正):即
generate_sun_angles_meeus_fixed,在标准 Meeus 算法的基础上加入了地心视差修正项。这是本文 Vala 代码最终采用的完整高精度方案。 - WikiImp (改进版维基百科算法):即
generate_sun_angles_wiki_improved,笔者基于 Wikipedia 的算法重新拟合了一组参数,引入了线性年份修正项。 - 傅里叶级数近似算法 (旧版实现):即
generate_sun_angles_fourier,这是笔者早期使用的一种基于傅里叶级数拟合的简化算法。 - 维基百科简化公式:即
generate_sun_angles_wikipedia,实现了维基百科上提供的简化版太阳赤纬和均时差公式。
通过计算每种算法结果与 astropy 基准值之间的均方根误差 (Root Mean Square Deviation, RMSD) 以及平均误差,我们可以量化它们的精度差异及系统偏差。
Spencer 傅里叶级数近似算法
这是笔者早期使用的 Vala 函数,它基于 Spencer 的傅里叶级数来近似太阳赤纬和均时差。这种方法实现相对简单,但精度有限,尤其是在长期时间跨度上。
/**
* Calculates solar elevation angles for each minute of the day.
*
* @param latitude_rad Latitude in radians.
* @param day_of_year Day of the year (1-365/366).
* @param year The year.
* @param longitude_deg Longitude in degrees.
* @param timezone_offset_hrs Timezone offset from UTC in hours.
*/
private void generate_sun_angles (double latitude_rad, int day_of_year, int year, double longitude_deg, double timezone_offset_hrs) {
double sin_lat = Math.sin (latitude_rad);
double cos_lat = Math.cos (latitude_rad);
double days_in_year = ((year % 4 == 0) && ((year % 100 != 0) || (year % 400 == 0))) ? 366.0 : 365.0;
for (int i = 0; i < RESOLUTION_PER_MIN; i += 1) {
// fractional_day_component: day of year plus fraction of the day
// -1 to avoid discontinuity at year start (Dec 31 to Jan 1)
double fractional_day_component = day_of_year - 1 + ((double) i) / RESOLUTION_PER_MIN;
// gamma: fractional year angle in radians
double gamma_rad = (2.0 * Math.PI / days_in_year) * fractional_day_component;
// Solar declination delta (rad) via Fourier series approximation
double decl_rad = 0.006918
- 0.399912 * Math.cos (gamma_rad)
+ 0.070257 * Math.sin (gamma_rad)
- 0.006758 * Math.cos (2.0 * gamma_rad)
+ 0.000907 * Math.sin (2.0 * gamma_rad)
- 0.002697 * Math.cos (3.0 * gamma_rad)
+ 0.001480 * Math.sin (3.0 * gamma_rad);
// Equation of Time (EoT) in minutes
double eqtime_minutes = 229.18 * (0.000075
+ 0.001868 * Math.cos (gamma_rad)
- 0.032077 * Math.sin (gamma_rad)
- 0.014615 * Math.cos (2.0 * gamma_rad)
- 0.040849 * Math.sin (2.0 * gamma_rad));
// True Solar Time (TST) in minutes, correcting local clock by EoT and longitude
double tst_minutes = i + eqtime_minutes + 4.0 * longitude_deg - 60.0 * timezone_offset_hrs;
// Hour angle H (°) relative to solar noon
double ha_deg = tst_minutes / 4.0 - 180.0;
double ha_rad = ha_deg * DEG2RAD;
// cos(phi): cosine of zenith angle via spherical trig
double cos_phi = sin_lat * Math.sin (decl_rad) + cos_lat * Math.cos (decl_rad) * Math.cos (ha_rad);
// clamp to valid range
cos_phi = cos_phi.clamp (-1.0, 1.0);
// Zenith angle phi (rad)
double phi_rad = Math.acos (cos_phi);
// Solar elevation alpha = 90° - phi, convert to degrees
double solar_elevation_rad = Math.PI / 2.0 - phi_rad;
sun_angles[i] = solar_elevation_rad * RAD2DEG;
}
}
维基百科的简化解析公式
维基百科上介绍的公式并非简单的数值拟合,而是从天体力学模型推导出的简化解析解。它根据实际轨道物理参数,对理想化的圆形轨道进行修正,来逼近真实的太阳位置。这类公式简单直观,但精度有限且忽略了轨道参数随年份的缓慢变化。笔者基于此公式进行了优化,详见《优化 Wikipedia 太阳位置简化公式》。
赤纬 ($\delta$)
- 从一个理想化的“平均太阳”出发,这个“平均太阳”在完美的圆形轨道上以恒定速度运动。
- 对上述理想模型加入最重要的修正项——由地球轨道椭圆形(偏心率)引起的速度变化。这个修正被称为中心差 (Equation of Center)。
- 将修正项代入,即可得到一个更精确的太阳黄经表达式,再通过坐标变换得到赤纬。
因此,这个公式是在一个简化的物理模型基础上,加入了关键的一阶修正,从而在不进行复杂计算的情况下,获得一个相对不错的精度。
这个公式实际上是先计算了近似的太阳黄经 $\lambda$,然后通过 $\delta = \arcsin\bigl(\sin(\varepsilon) \cdot \sin(\lambda)\bigr)$ 得到。维基百科给出的合并形式如下:
\[\delta_\odot = \arcsin \left [ \sin \left ( -23.44^\circ \right ) \cdot \cos \left ( \frac{360^\circ}{365.24} \left (N + 10 \right ) + \frac{360^\circ}{\pi} \cdot 0.0167 \sin \left ( \frac{360^\circ}{365.24} \left ( N - 2 \right ) \right ) \right ) \right ]\]其中各参数的物理意义如下:
- $-23.44^\circ$:地球的黄赤交角 $\varepsilon$,决定了太阳赤纬的最大变化范围。
- $N$:从当年1月1日午夜UT起算的年积日(例如,1月1日 $N=0$,1月2日 $N=1$)。
- $\dfrac{360^\circ}{365.24}$:地球公转的平均角速度(度/天)。
- $N + 10$:表达式 $(N + 10)$ 用于近似计算从冬至(太阳赤纬最低点)起算的天数,因为冬至大约在12月22日,比1月1日早10天。
- $0.0167$:地球轨道的偏心率 $e$,描述了轨道偏离正圆的程度。
- $N - 2$:表达式 $(N - 2)$ 用于近似计算从近日点(地球离太阳最近的点)起算的天数,因为近日点约在1月3日,比1月1日晚2天。
- $\displaystyle \frac{360^\circ}{\pi} \cdot 0.0167 \cdot \sin(\dots)$:此项是中心差的一阶近似,用于修正因轨道偏心率导致太阳视运动速度不均匀的问题。
带入常数,简化可得:
\[\delta_\odot = - \arcsin \left [ 0.39779 \cos \left ( 0.98565^\circ \left (N + 10 \right ) + 1.914^\circ \sin \left ( 0.98565^\circ \left ( N - 2 \right ) \right ) \right ) \right ]\]均时差 (EoT)
同样,均时差也可以通过一个包含两个主要周期项的简化公式来近似:
\[\Delta t_{ey} = -7.659\sin(D) + 9.863\sin \left(2D + 3.5932 \right) \quad [\text{minutes}]\]其中:
- $-7.659 \sin(D)$:此项是主要由地球轨道偏心率引起的周期性变化,周期为一年。
- $9.863 \sin(2D + \dots)$:此项是主要由黄赤交角引起的周期性变化,周期为半年。
而 $D$ 本身是一个随时间均匀增加的角度,其定义为:
\[D = 6.24004077 + 0.01720197(365.25(y-2000) + d)\]其中,$d$ 是从当年1月1日开始计算的天数,$y$ 是当前年份。$D$ 的起始值和增长率与地球的平黄经和平近点角相关,是计算上述两个周期性修正的基础。
Python 验证脚本
以下是用于生成对比数据的完整 Python 脚本。它依赖 numpy 和 astropy 库。除了这里列出的几种算法外,笔者还基于 Wikipedia 的算法重新拟合了一组参数,命名为 WikiImp(改进版维基百科算法),详细的优化过程和原理请参见《优化 Wikipedia 太阳位置简化公式》。
该脚本的核心逻辑是以天文学界公认的专业库 Astropy 作为真值,对笔者收集和实现的五种不同算法(包括经典的 Jean Meeus 算法、傅里叶级数拟合以及改进版的 Wikipedia 公式)进行准确性测试。
这个验证框架具备以下特点:
- 全时空覆盖:默认测试范围横跨 1975 年至 2075 年,取其中每个整点的数据,涵盖高中低纬度,从赤道(新加坡)到极点(南极),从东八区(北京)到零时区的所有典型地理位置,总共包含了 5,312,160 个数据点。
- 数据驱动:计算均方根误差 (RMSD)、95% 分位数误差及最大绝对误差,并自动生成误差分布直方图 (SVG)。
- 误差分布验证:脚本绘制了误差的频率直方分布。正是通过这个脚本的直方图分析,笔者成功捕捉到了早期算法中存在的 0.002° 地心视差系统性偏差,并验证了修正后的 MeeusFixed 算法已达到近乎完美的零系统偏差分布。
代码说明:在测试脚本中,
generate_sun_angles_meeus对应未加视差修正的 Meeus 算法,generate_sun_angles_meeus_fixed对应加入了地心视差修正的完整版本。两者均使用 Meeus 原书参数。
#!/usr/bin/env python3
import numpy as np
import datetime
import calendar
from astropy.coordinates import EarthLocation, AltAz, get_sun
from astropy.time import Time
from astropy.utils.iers import IERS_B, conf
import matplotlib.pyplot as plt
import argparse
import os
conf.iers_active = IERS_B.open()
DEG2RAD = np.pi / 180.0
RAD2DEG = 180.0 / np.pi
LOCATIONS = {
"Beijing": {"lat": 39.9075, "lon": 116.3972, "tz": 8.0},
"Chongqing": {"lat": 29.5628, "lon": 106.5528, "tz": 8.0},
"Singapore": {"lat": 1.3521, "lon": 103.8198, "tz": 8.0},
"Sydney": {"lat": -33.8688, "lon": 151.2093, "tz": 10.0},
"Stockholm": {"lat": 59.3293, "lon": 18.0686, "tz": 1.0},
"South Pole": {"lat": -90.0, "lon": 0.0, "tz": 0.0}
}
# --- Calculation Functions (Unchanged) ---
def astropy_sun_elevations(year, month, day, latitude_deg, longitude_deg, timezone_offset_hrs):
location = EarthLocation(lat=latitude_deg, lon=longitude_deg)
angles = []
for local_hour in range(24):
local_dt = datetime.datetime(year, month, day, local_hour, 0, 0)
utc_dt = local_dt - datetime.timedelta(hours=timezone_offset_hrs)
time_astropy = Time(utc_dt)
altaz_frame = AltAz(obstime=time_astropy, location=location)
sun_altaz = get_sun(time_astropy).transform_to(altaz_frame)
angles.append(sun_altaz.alt.degree)
return np.array(angles)
def generate_sun_angles_meeus(latitude_deg, longitude_deg, timezone_offset_hrs, year, month, day):
julian_date = float(datetime.date(year, month, day).toordinal())
latitude_rad = latitude_deg * DEG2RAD
sin_lat = np.sin(latitude_rad)
cos_lat = np.cos(latitude_rad)
base_days_from_epoch = julian_date - 730120.5
base_days_sq = base_days_from_epoch ** 2
base_days_cb = base_days_sq * base_days_from_epoch
obliquity_deg = 23.439291111 - 3.560347e-7 * base_days_from_epoch - 1.2285e-16 * base_days_sq + 1.0335e-20 * base_days_cb
obliquity_sin = np.sin(obliquity_deg * DEG2RAD)
obliquity_cos = np.cos(obliquity_deg * DEG2RAD)
ecliptic_c1 = 1.914602 - 1.3188e-7 * base_days_from_epoch - 1.049e-14 * base_days_sq
ecliptic_c2 = 0.019993 - 2.7652e-9 * base_days_from_epoch
ecliptic_c3 = 0.000289
tst_offset = 4.0 * longitude_deg - 60.0 * timezone_offset_hrs
angles = []
for local_hour in range(24):
i = local_hour * 60
time_offset_days = (i / 60.0 - timezone_offset_hrs) / 24.0
days_from_epoch = base_days_from_epoch + time_offset_days
days_from_epoch_sq = days_from_epoch ** 2
days_from_epoch_cb = days_from_epoch_sq * days_from_epoch
mean_anomaly_deg = 357.52772 + 0.985600282 * days_from_epoch - 1.2016e-13 * days_from_epoch_sq - 6.835e-20 * days_from_epoch_cb
mean_anomaly_deg = np.fmod(mean_anomaly_deg, 360.0)
mean_longitude_deg = 280.46645 + 0.98564736 * days_from_epoch + 2.2727e-13 * days_from_epoch_sq
mean_longitude_deg = np.fmod(mean_longitude_deg, 360.0)
mean_anomaly_rad = mean_anomaly_deg * DEG2RAD
ecliptic_longitude_deg = (mean_longitude_deg + ecliptic_c1 * np.sin(mean_anomaly_rad) + ecliptic_c2 * np.sin(2 * mean_anomaly_rad) + ecliptic_c3 * np.sin(3 * mean_anomaly_rad))
ecliptic_longitude_rad = ecliptic_longitude_deg * DEG2RAD
declination_sin = np.clip(obliquity_sin * np.sin(ecliptic_longitude_rad), -1.0, 1.0)
declination_cos = np.sqrt(1.0 - declination_sin ** 2)
right_ascension_rad = np.arctan2(obliquity_cos * np.sin(ecliptic_longitude_rad), np.cos(ecliptic_longitude_rad))
right_ascension_hours = (right_ascension_rad * RAD2DEG) / 15.0
mean_time = np.fmod(mean_longitude_deg / 15.0, 24.0)
delta_ra = right_ascension_hours - mean_time
if delta_ra > 12.0: right_ascension_hours -= 24.0
elif delta_ra < -12.0: right_ascension_hours += 24.0
eqtime_minutes = (mean_time - right_ascension_hours) * 60.0
tst_minutes = i + eqtime_minutes + tst_offset
hour_angle_rad = (tst_minutes / 4.0 - 180.0) * DEG2RAD
elevation_sine = sin_lat * declination_sin + cos_lat * declination_cos * np.cos(hour_angle_rad)
elevation = np.arcsin(np.clip(elevation_sine, -1.0, 1.0)) * RAD2DEG
angles.append(elevation)
return np.array(angles)
def generate_sun_angles_meeus_fixed(latitude_deg, longitude_deg, timezone_offset_hrs, year, month, day):
julian_date = float(datetime.date(year, month, day).toordinal())
latitude_rad = latitude_deg * DEG2RAD
sin_lat = np.sin(latitude_rad)
cos_lat = np.cos(latitude_rad)
base_days_from_epoch = julian_date - 730120.5
base_days_sq = base_days_from_epoch ** 2
base_days_cb = base_days_sq * base_days_from_epoch
obliquity_deg = 23.439291111 - 3.560347e-7 * base_days_from_epoch - 1.2285e-16 * base_days_sq + 1.0335e-20 * base_days_cb
obliquity_sin = np.sin(obliquity_deg * DEG2RAD)
obliquity_cos = np.cos(obliquity_deg * DEG2RAD)
ecliptic_c1 = 1.914602 - 1.3188e-7 * base_days_from_epoch - 1.049e-14 * base_days_sq
ecliptic_c2 = 0.019993 - 2.7652e-9 * base_days_from_epoch
ecliptic_c3 = 0.000289
tst_offset = 4.0 * longitude_deg - 60.0 * timezone_offset_hrs
angles = []
for local_hour in range(24):
i = local_hour * 60
time_offset_days = (i / 60.0 - timezone_offset_hrs) / 24.0
days_from_epoch = base_days_from_epoch + time_offset_days
days_from_epoch_sq = days_from_epoch ** 2
days_from_epoch_cb = days_from_epoch_sq * days_from_epoch
mean_anomaly_deg = 357.52772 + 0.985600282 * days_from_epoch - 1.2016e-13 * days_from_epoch_sq - 6.835e-20 * days_from_epoch_cb
mean_anomaly_deg = np.fmod(mean_anomaly_deg, 360.0)
mean_longitude_deg = 280.46645 + 0.98564736 * days_from_epoch + 2.2727e-13 * days_from_epoch_sq
mean_longitude_deg = np.fmod(mean_longitude_deg, 360.0)
mean_anomaly_rad = mean_anomaly_deg * DEG2RAD
ecliptic_longitude_deg = (mean_longitude_deg + ecliptic_c1 * np.sin(mean_anomaly_rad) + ecliptic_c2 * np.sin(2 * mean_anomaly_rad) + ecliptic_c3 * np.sin(3 * mean_anomaly_rad))
ecliptic_longitude_rad = ecliptic_longitude_deg * DEG2RAD
declination_sin = np.clip(obliquity_sin * np.sin(ecliptic_longitude_rad), -1.0, 1.0)
declination_cos = np.sqrt(1.0 - declination_sin ** 2)
right_ascension_rad = np.arctan2(obliquity_cos * np.sin(ecliptic_longitude_rad), np.cos(ecliptic_longitude_rad))
right_ascension_hours = (right_ascension_rad * RAD2DEG) / 15.0
mean_time = np.fmod(mean_longitude_deg / 15.0, 24.0)
delta_ra = right_ascension_hours - mean_time
if delta_ra > 12.0: right_ascension_hours -= 24.0
elif delta_ra < -12.0: right_ascension_hours += 24.0
eqtime_minutes = (mean_time - right_ascension_hours) * 60.0
tst_minutes = i + eqtime_minutes + tst_offset
hour_angle_rad = (tst_minutes / 4.0 - 180.0) * DEG2RAD
elevation_sin = np.clip(sin_lat * declination_sin + cos_lat * declination_cos * np.cos(hour_angle_rad), -1.0, 1.0)
elevation_cos = np.sqrt(1.0 - elevation_sin * elevation_sin)
geocentric_parallax_deg = 0.00244 * elevation_cos
elevation = np.arcsin(elevation_sin) * RAD2DEG - geocentric_parallax_deg
angles.append(elevation)
return np.array(angles)
def generate_sun_angles_fourier(latitude_deg, longitude_deg, timezone_offset_hrs, year, month, day):
latitude_rad = latitude_deg * DEG2RAD
sin_lat = np.sin(latitude_rad)
cos_lat = np.cos(latitude_rad)
dt = datetime.date(year, month, day)
day_of_year = dt.timetuple().tm_yday
days_in_year = 366.0 if calendar.isleap(year) else 365.0
angles = []
for local_hour in range(24):
i = local_hour * 60
fractional_day_component = day_of_year - 1 + (i / 1440.0)
gamma_rad = (2.0 * np.pi / days_in_year) * fractional_day_component
decl_rad = 0.006918 - 0.399912 * np.cos(gamma_rad) + 0.070257 * np.sin(gamma_rad) - 0.006758 * np.cos(2.0 * gamma_rad) + 0.000907 * np.sin(2.0 * gamma_rad) - 0.002697 * np.cos(3.0 * gamma_rad) + 0.001480 * np.sin(3.0 * gamma_rad)
eqtime_minutes = 229.18 * (0.000075 + 0.001868 * np.cos(gamma_rad) - 0.032077 * np.sin(gamma_rad) - 0.014615 * np.cos(2.0 * gamma_rad) - 0.040849 * np.sin(2.0 * gamma_rad))
tst_minutes = i + eqtime_minutes + 4.0 * longitude_deg - 60.0 * timezone_offset_hrs
ha_rad = (tst_minutes / 4.0 - 180.0) * DEG2RAD
elevation_sine = sin_lat * np.sin(decl_rad) + cos_lat * np.cos(decl_rad) * np.cos(ha_rad)
elevation = np.arcsin(np.clip(elevation_sine, -1.0, 1.0)) * RAD2DEG
angles.append(elevation)
return np.array(angles)
def generate_sun_angles_wikipedia(latitude_deg, longitude_deg, timezone_offset_hrs, year, month, day):
latitude_rad = latitude_deg * DEG2RAD
sin_lat = np.sin(latitude_rad)
cos_lat = np.cos(latitude_rad)
dt = datetime.date(year, month, day)
day_of_year = dt.timetuple().tm_yday
angles = []
for local_hour in range(24):
utc_hour = local_hour - timezone_offset_hrs
N = day_of_year - 1 + utc_hour / 24.0
arg1_deg = 0.98565 * (N + 10)
arg2_deg = 0.98565 * (N - 2)
cos_arg_deg = arg1_deg + 1.914 * np.sin(arg2_deg * DEG2RAD)
decl_rad = -np.arcsin(0.39779 * np.cos(cos_arg_deg * DEG2RAD))
d_eot = day_of_year - 1
D_rad = 6.24004077 + 0.01720197 * (365.25 * (year - 2000) + d_eot)
eqtime_minutes = -7.659 * np.sin(D_rad) + 9.863 * np.sin(2 * D_rad + 3.5932)
i = local_hour * 60
tst_minutes = i + eqtime_minutes + 4.0 * longitude_deg - 60.0 * timezone_offset_hrs
ha_rad = (tst_minutes / 4.0 - 180.0) * DEG2RAD
elevation_sine = sin_lat * np.sin(decl_rad) + cos_lat * np.cos(decl_rad) * np.cos(ha_rad)
elevation = np.arcsin(np.clip(elevation_sine, -1.0, 1.0)) * RAD2DEG
angles.append(elevation)
return np.array(angles)
def generate_sun_angles_wiki_improved(latitude_deg, longitude_deg, timezone_offset_hrs, year, month, day):
latitude_rad = latitude_deg * DEG2RAD
sin_lat = np.sin(latitude_rad)
cos_lat = np.cos(latitude_rad)
dt = datetime.date(year, month, day)
day_of_year = dt.timetuple().tm_yday
obli_const = 23.689615119428524
obli_year = -0.0001272039401833378
sol_const = -4.953654511287448
sol_year = 0.007584740998948542
peri_const = 16.907638765610766
peri_year = -0.009931455309012382
ecc_const = 0.017494322009221987
ecc_year = -4.274172671320393e-07
eot_ecc_amp_const = -7.5281042369998135
eot_ecc_amp_year = 9.320261665981816e-05
eot_obli_amp_const = 10.175305445225787
eot_obli_amp_year = -0.0001329535053396791
eot_obli_phase_const = 2.3439927750958214
eot_obli_phase_year = 0.0006426678778734212
eot_dconst_const = 6.266288107936987
eot_dconst_year = -2.7626758599300164e-05
OMEGA_DEG_PER_DAY = 360.0 / 365.2422
OMEGA_D_RAD_PER_DAY = 0.01720197
TROPICAL_YEAR_DAYS = 365.25
ecc_factor = 360.0 / np.pi * (ecc_const + ecc_year * year)
solstice_offset = sol_const + sol_year * year
perihelion_offset = peri_const + peri_year * year
sin_obliquity_neg = np.sin( - (obli_const + obli_year * year) * DEG2RAD )
tropical_offset = TROPICAL_YEAR_DAYS * (year - 2000.0)
eot_dconst = eot_dconst_const + eot_dconst_year * year
eot_ecc_amp = eot_ecc_amp_const + eot_ecc_amp_year * year
eot_obli_amp = eot_obli_amp_const + eot_obli_amp_year * year
eot_obli_phase = eot_obli_phase_const + eot_obli_phase_year * year
tst_offset = 4.0 * longitude_deg - 60.0 * timezone_offset_hrs
angles = []
for local_hour in range(24):
i = local_hour * 60
fractional_day_component = day_of_year - 1 + (i / 1440.0)
sin_decl = sin_obliquity_neg * np.cos((OMEGA_DEG_PER_DAY * (fractional_day_component + solstice_offset) + ecc_factor * np.sin(OMEGA_DEG_PER_DAY * (fractional_day_component + perihelion_offset) * DEG2RAD)) * DEG2RAD)
sin_decl = np.clip(sin_decl, -1.0, 1.0)
cos_decl = np.sqrt(1.0 - sin_decl ** 2)
d_rad = eot_dconst + OMEGA_D_RAD_PER_DAY * (tropical_offset + fractional_day_component)
eqtime_minutes = eot_ecc_amp * np.sin(d_rad) + eot_obli_amp * np.sin(2.0 * d_rad + eot_obli_phase)
tst_minutes = i + eqtime_minutes + tst_offset
ha_rad = (tst_minutes / 4.0 - 180.0) * DEG2RAD
elevation_sine = sin_lat * sin_decl + cos_lat * cos_decl * np.cos(ha_rad)
elevation = np.arcsin(np.clip(elevation_sine, -1.0, 1.0)) * RAD2DEG
angles.append(elevation)
return np.array(angles)
# --- Statistical Helpers ---
def calculate_rmsd(errors):
"""Calculates scientifically correct RMSD from a list of errors."""
if len(errors) == 0:
return 0.0
return np.sqrt(np.mean(np.array(errors) ** 2))
def main():
parser = argparse.ArgumentParser(description="Test solar angle accuracy with scientifically correct RMSD aggregation")
parser.add_argument('--start-year', type=int, default=1975, help='Start year for the test range')
parser.add_argument('--end-year', type=int, default=2075, help='End year for the test range')
parser.add_argument('--interval', type=int, default=1, help='Year interval for the test range')
parser.add_argument('--day-interval', type=int, default=1, help='Day interval within each month')
parser.add_argument('--mode', choices=['generate', 'validate'], default='validate', help='generate or validate')
parser.add_argument('--data-file', type=str, default='astropy_cache.npz', help='NPZ file for astropy reference data')
args = parser.parse_args()
years = list(range(args.start_year, args.end_year + 1, args.interval))
methods = ['Meeus', 'Fourier', 'Wikipedia', 'WikiImp', 'MeeusFixed']
# Initialize collections.
# Instead of storing averaged RMSDs, we store raw errors (diffs) to compute global RMSD correctly later.
location_diffs = {m: {loc: [] for loc in LOCATIONS} for m in methods}
month_diffs = {m: [[] for _ in range(12)] for m in methods}
year_diffs = {m: {y: [] for y in years} for m in methods}
all_diffs = {m: [] for m in methods} # Global collection
month_names = [datetime.date(2000, i+1, 1).strftime('%b') for i in range(12)]
if args.mode == 'generate':
print("Generating Astropy reference data...")
astro_data = {}
total_computed = 0
for location_name, params in LOCATIONS.items():
lat, lon, tz = params["lat"], params["lon"], params["tz"]
for year in years:
for month in range(1, 13):
_, days_in_month = calendar.monthrange(year, month)
for day in range(1, days_in_month + 1, args.day_interval):
print(f"Computing {location_name} {year}-{month:02d}-{day:02d}... ({total_computed})", end='\r')
angles = astropy_sun_elevations(year, month, day, lat, lon, tz)
key = f"{location_name}_{year}_{month}_{day}"
astro_data[key] = angles
total_computed += 1
np.savez_compressed(args.data_file, **astro_data)
print(f"\nAstropy data saved to {args.data_file} (total {len(astro_data)} entries)")
return
# Validate mode
if not os.path.exists(args.data_file):
print(f"Error: Astropy data file '{args.data_file}' not found.")
return
astro_data = dict(np.load(args.data_file, allow_pickle=True).items())
print(f"Loaded astropy data from {args.data_file} ({len(astro_data)} entries)")
for location_name, params in LOCATIONS.items():
lat, lon, tz = params["lat"], params["lon"], params["tz"]
print(f"\n{'='*90}")
print(f"Validation Results for: {location_name}")
print(f"(Lat: {lat}, Lon: {lon}, TZ: UTC{tz:+.1f})")
print(f"{'='*90}")
for year in years:
print(f"\n--- Year: {year} ---")
print(f"| {'Mon(d)':<7} | {'Meeus RMSD':<12} | {'Fourier RMSD':<13} | {'Wiki RMSD':<11} | {'Wiki Imp RMSD':<14} | {'MeeusFixed RMSD':<15} |")
print(f"|{'-'*9}|{'-'*14}|{'-'*15}|{'-'*13}|{'-'*16}|{'-'*17}|")
# Temporary accumulators for the Year table summary
current_year_diffs = {m: [] for m in methods}
for month in range(1, 13):
_, days_in_month = calendar.monthrange(year, month)
# Temporary accumulators for the Month row
current_month_diffs = {m: [] for m in methods}
num_days_computed = 0
for day in range(1, days_in_month + 1, args.day_interval):
key = f"{location_name}_{year}_{month}_{day}"
if key not in astro_data:
continue
astro_angles = astro_data[key]
# Generate angles
calc_funcs = {
'Meeus': generate_sun_angles_meeus,
'Fourier': generate_sun_angles_fourier,
'Wikipedia': generate_sun_angles_wikipedia,
'WikiImp': generate_sun_angles_wiki_improved,
'MeeusFixed': generate_sun_angles_meeus_fixed
}
results = {}
for m, func in calc_funcs.items():
calc_angles = func(lat, lon, tz, year, month, day)
diffs = calc_angles - astro_angles
results[m] = diffs
# Store raw errors for statistical aggregation
# 1. For current month printout
current_month_diffs[m].extend(diffs)
# 2. For current year printout
current_year_diffs[m].extend(diffs)
# 3. For Global stats
all_diffs[m].extend(diffs)
# 4. For Location stats
location_diffs[m][location_name].extend(diffs)
# 5. For Month stats (aggregated across years/locs)
month_diffs[m][month-1].extend(diffs)
# 6. For Year stats (aggregated across locs)
year_diffs[m][year].extend(diffs)
num_days_computed += 1
if num_days_computed > 0:
# Calculate scientifically correct RMSD for the month row
# sqrt(sum(errors^2) / count)
row_vals = [calculate_rmsd(current_month_diffs[m]) for m in methods]
month_name = datetime.date(year, month, 1).strftime('%b')
print(f"| {month_name}({num_days_computed:<2}) | {row_vals[0]:<12.4f} | {row_vals[1]:<13.4f} | {row_vals[2]:<11.4f} | {row_vals[3]:<14.4f} | {row_vals[4]:<15.4f} |")
# Calculate scientifically correct RMSD for the year average row
year_vals = [calculate_rmsd(current_year_diffs[m]) for m in methods]
print(f"|{'-'*9}|{'-'*14}|{'-'*15}|{'-'*13}|{'-'*16}|{'-'*17}|")
print(f"| {'RMSD':<7} | {year_vals[0]:<12.4f} | {year_vals[1]:<13.4f} | {year_vals[2]:<11.4f} | {year_vals[3]:<14.4f} | {year_vals[4]:<15.4f} |")
# --- Scientific Statistics Aggregation ---
# Global Statistics
print(f"\n{'='*80}")
print("GLOBAL STATISTICS ACROSS ALL DATA POINTS")
print(f"{'='*80}")
print("| Method | Global RMSD | 95% Abs Error | Global Max Error | Mean Error |")
print("|------------|-------------|---------------|------------------|-------------|")
for m in methods:
diffs_array = np.array(all_diffs[m])
global_rmsd = np.sqrt(np.mean(diffs_array ** 2))
global_p95 = np.percentile(np.abs(diffs_array), 95)
global_max_error = np.max(np.abs(diffs_array))
global_mean_error = np.mean(diffs_array)
print(f"| {m:<10} | {global_rmsd:<11.4e} | {global_p95:<13.4e} | {global_max_error:<16.4e} | {global_mean_error:<11.4e} |")
# Statistics by Location (Corrected Calculation)
print(f"\n{'='*80}")
print("STATISTICS BY LOCATION (Scientific RMSD)")
print(f"{'='*80}")
for location_name in LOCATIONS:
print(f"\n{location_name}:")
print("| Method | Total RMSD | Max Error |")
print("|------------|--------------|------------|")
for m in methods:
diffs = location_diffs[m][location_name]
rmsd = calculate_rmsd(diffs)
worst = np.max(np.abs(diffs)) if len(diffs) > 0 else 0
print(f"| {m:<10} | {rmsd:<12.4f} | {worst:<10.4f} |")
# Statistics by Month (Corrected Calculation)
print(f"\n{'='*80}")
print("STATISTICS BY MONTH (Scientific RMSD across all years/locs)")
print(f"{'='*80}")
print(f"| {'Month':<5} | {'Meeus':<10} | {'Fourier':<10} | {'Wiki':<10} | {'WikiImp':<10} | {'MeeusFix':<10} |")
print(f"|{'-'*7}|{'-'*12}|{'-'*12}|{'-'*12}|{'-'*12}|{'-'*12}|")
for mon in range(12):
row_str = f"| {month_names[mon]:<5} |"
for m in methods:
diffs = month_diffs[m][mon]
rmsd = calculate_rmsd(diffs)
row_str += f" {rmsd:<10.4f} |"
print(row_str)
# Statistics by Year (Corrected Calculation)
print(f"\n{'='*80}")
print("STATISTICS BY YEAR (Scientific RMSD across all locs)")
print(f"{'='*80}")
print(f"| {'Year':<4} | {'Meeus':<10} | {'Fourier':<10} | {'Wiki':<10} | {'WikiImp':<10} | {'MeeusFix':<10} |")
print(f"|{'-'*6}|{'-'*12}|{'-'*12}|{'-'*12}|{'-'*12}|{'-'*12}|")
for y in years:
row_str = f"| {y:<4} |"
for m in methods:
diffs = year_diffs[m][y]
rmsd = calculate_rmsd(diffs)
row_str += f" {rmsd:<10.4f} |"
print(row_str)
# Histogram Generation (Unchanged logic, just utilizing clean data)
print(f"\n{'='*80}")
print("Generating histograms...")
for m in methods:
diffs_array = np.array(all_diffs[m])
abs_diffs_array = np.abs(diffs_array)
rmsd = np.sqrt(np.mean(diffs_array ** 2))
p95 = np.percentile(abs_diffs_array, 95)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
ax1.hist(diffs_array, bins='auto', alpha=0.7, color='skyblue')
spine_lw = ax1.spines['left'].get_linewidth()
ax1.axvline(0, color='black', linestyle='-', linewidth=spine_lw, label='Zero Deviation')
ax1.axvline(np.mean(diffs_array), color='orange', linestyle='--', linewidth=2, label=f'Mean: {np.mean(diffs_array):.4f}')
ax1.set_title(f'Error Distribution')
ax1.set_xlabel('Error (degrees)')
ax1.set_ylabel('Frequency')
ax1.legend()
ax2.hist(abs_diffs_array, bins='auto', alpha=0.7, color='lightgreen')
ax2.axvline(rmsd, color='orange', linestyle='--', linewidth=2, label=f'RMSD: {rmsd:.4f}')
ax2.axvline(p95, color='blue', linestyle='--', linewidth=2, label=f'95% abs: {p95:.4f}')
ax2.set_title(f'Absolute Error Distribution')
ax2.set_xlabel('Abs Error (degrees)')
ax2.set_ylabel('Frequency')
ax2.legend()
plt.suptitle(f'{m} Solar Elevation Error')
plt.tight_layout()
plt.savefig(f'{m}_error_histogram.svg', dpi=300, bbox_inches='tight')
plt.close()
if __name__ == "__main__":
main()
验证结果与分析
综合对比
首先从海量数据中提炼出核心指标。
| 性能指标 (单位: 度) | MeeusFixed (含视差) | Meeus (无视差) | WikiImp | Fourier | Wikipedia |
|---|---|---|---|---|---|
| 全局 RMSD | 0.0030 | 0.0036 | 0.0865 | 0.1265 | 0.1819 |
| 95% 绝对误差 | 0.0058 | 0.0070 | 0.1738 | 0.2687 | 0.3703 |
| 全局最大误差 | 0.0121 | 0.0145 | 0.2864 | 0.4853 | 0.6415 |
| 平均误差 (Bias) | -0.0000 | 0.0020 | 0.0018 | 0.0041 | 0.0024 |
 |
|---|
| Meeus 算法(含视差修正)误差分布直方图 |
 |
| Meeus 算法(无视差修正)误差分布直方图 |
 |
| 傅里叶级数算法误差分布直方图 |
 |
| 维基百科算法误差分布直方图 |
- MeeusFixed (含视差修正) 展现了惊人的精度,其全局 RMSD 仅为 0.0030°。最关键的是,其平均误差为 $-1.8 \times 10^{-7}$,几乎为 0,进一步定量计算可知其系统误差显著性 $Z = -0.14$,其绝对值远远小于95%置信水平临界值 1.96,说明加入了视差修正后,消除了系统性偏差。
- Meeus (无视差修正) 的精度也非常高 (RMSD 0.0036°),但存在一个约 0.0020° 的正向平均误差。这正是地心视差的影响(计算出的地心高度角总是略高于地表观测到的高度角)。这一对比有力地证明了在高精度计算中引入视差修正的必要性。
- WikiImp (改进版维基百科算法) 平均 RMSD 为 0.0710°,优于傅里叶算法,但仍远逊于 Meeus 算法。
- Meeus 算法的最差表现 (0.0121°) 依然比其他算法的平均表现好得多。
地理位置对比
| 地点 | MeeusFixed (RMSD/Max) | Meeus (RMSD/Max) | WikiImp (RMSD/Max) | Fourier (RMSD/Max) | Wikipedia (RMSD/Max) |
|---|---|---|---|---|---|
| Beijing | 0.0030 / 0.0115 | 0.0036 / 0.0138 | 0.0764 / 0.2127 | 0.1014 / 0.3704 | 0.1844 / 0.6270 |
| Chongqing | 0.0031 / 0.0120 | 0.0037 / 0.0143 | 0.0747 / 0.2121 | 0.0956 / 0.3701 | 0.1676 / 0.6303 |
| Singapore | 0.0031 / 0.0121 | 0.0036 / 0.0145 | 0.0681 / 0.2140 | 0.0795 / 0.3694 | 0.1244 / 0.6195 |
| Sydney | 0.0031 / 0.0117 | 0.0036 / 0.0131 | 0.0798 / 0.2459 | 0.0899 / 0.3421 | 0.1734 / 0.6415 |
| Stockholm | 0.0029 / 0.0100 | 0.0036 / 0.0124 | 0.0998 / 0.2864 | 0.1658 / 0.4818 | 0.2068 / 0.6344 |
| South Pole | 0.0028 / 0.0073 | 0.0036 / 0.0098 | 0.1118 / 0.2735 | 0.1861 / 0.4853 | 0.2192 / 0.5670 |
Meeus 算法具有完美的地理普适性,从赤道到极点都保持极高精度。加入视差修正后的 MeeusFixed 在所有地点均有一致的性能提升。
年份对比
通过对比 1975 年和 2075 年的数据,评估算法的长期稳定性。
| 方法 | 1975年 RMSD (°) | 2075年 RMSD (°) | 趋势分析 |
|---|---|---|---|
| MeeusFixed | 0.0029 | 0.0031 | 精度在百年尺度上保持极高稳定性。 |
| Meeus | 0.0036 | 0.0039 | 稳定性同上,系统误差恒定存在。 |
| WikiImp | 0.0565 | 0.0564 | 改进版算法引入了年份修正,保持了长期稳定。 |
| Fourier | 0.0805 | 0.1350 | 误差随时间显著增加(增长约 68%)。 |
| Wikipedia | 0.0727 | 0.2205 | 误差随时间剧烈增加(增长约 203%)。 |
Meeus 算法包含了对地球轨道参数长期变化的修正项,因此其精度在很长的时间跨度内都是可靠的。WikiImp 通过引入年份修正也保持了长期稳定。而傅里叶和原始维基百科算法是基于特定历元的经验公式,离拟合年代越远,误差越大。
月份/季节维度分析
- Meeus / MeeusFixed: 月度 RMSD 波动极小,表现出极佳的稳定性。
- Fourier: 波动巨大,6月和12月表现较好(~0.05~0.06),但 3月和 9月 误差飙升至 0.16~0.18 左右。
- Wikipedia: 同样波动巨大,6月和12月较好(~0.06~0.07),但 3月和 9月 误差高达 0.25~0.26。
- WikiImp: 相比原始版有很大改进,但仍有季节性波动,6月最佳(0.0249),3月最差(0.1167)。
这表明 Meeus 算法精确地模拟了地球公转的真实物理过程,而简化模型未能精确模拟地球在椭圆轨道上运动速度的变化,导致均时差和太阳赤纬的季节性变化计算不准。
结论
Meeus 算法是一个基于天体力学的物理模型,在所有测试维度(时间、地点、季节)上都展现了压倒性的精度优势和稳定性。特别是 MeeusFixed (含视差修正) 版本,通过引入地心视差修正,消除了约 0.0020° 的系统误差,实现了 RMSD 0.0030° 的极致精度。这证明了在追求高精度数值计算时,物理模型的完整性至关重要。
WikiImp 是笔者对维基百科算法的优化版本,详细介绍请参见《优化 Wikipedia 太阳位置简化公式》。它通过引入线性年份修正项,解决了长期漂移问题并提升了整体精度,但仍受限于物理模型的简化,无法达到 Meeus 的高度。
傅里叶级数算法和原始维基百科算法则存在明显的局限性,仅适用于对精度要求不高且时间跨度较短的场景。